I have spent significant amount of time to figure out how to create algorithm for

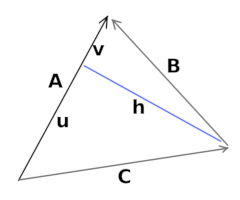
we have

• u^2 h^2 = C^2
• v^2 h^2 = B^2
• A = u v

then given the A vector we can find the opposite vertex and make two new ones bases.

Using brute force (we can use some heuristic but the problem states that n will be less than 9, then:

public class ConstructionToy {
    static class V2 { double x, y; V2(double X, double Y) { x = X; y = Y; } }
    static class Vec { V2 from, to; double length; Vec(V2 f, V2 t, double l) {from = f; to = t; length = l; } }
    static V2 sub(V2 a, V2 b) { return new V2(a.x - b.x, a.y - b.y); }
    static V2 sum(V2 a, V2 b) { return new V2(a.x   b.x, a.y   b.y); }
    static V2 mul(V2 a, double k) { return new V2(a.x * k, a.y * k); }
    static class Step { Vec e1, e2; V2 vertex; Step(Vec E1, Vec E2, V2 vx) { e1 = E1; e2 = E2; vertex = vx; }}

    // triangle with base A adding edges B and C generate new two bases (over B and over C)
    // triangle is generated on the clockwise side of A vector
    static Step next(Vec A, double B, double C) {
        V2 delta = sub(A.to, A.from);
        V2 vec = mul(delta, 1.0 / A.length);
        V2 tan = new V2(vec.y, -vec.x);
        double v = (A.length * A.length - B * B   C * C) / (2 * A.length); // could be optimized memoizing
        double h2 = C * C - v * v;
        if(h2 < 0.0)
            return null;
        double h = Math.sqrt(h2);
        V2 vertex = sum(sum(A.from, mul(vec, v)), mul(tan, h));
        return new Step(new Vec(vertex, A.to, B), new Vec(A.from, vertex, C), vertex);
    }

    static double bruteForce(double [] edges, Set<Integer> used, Vec base) {
        if(edges.length - used.size() < 2)
            return 0.0;
        double max = 0.0;
        // for every two (not used) edges we can construct a new triangle
        for(int i = 0; i < edges.length; i  )
            if(!used.contains(i)) {
                used.add(i);
                for (int j = 0; j < edges.length; j  )
                    if(!used.contains(j)) {
                        used.add(j);
                        Step s = next(base, edges[i], edges[j]);
                        if(s != null) {
                            max = Math.max(max, s.vertex.x);
                            max = Math.max(max, bruteForce(edges, used, s.e1));
                            max = Math.max(max, bruteForce(edges, used, s.e2));
                            max = Math.max(max, bruteForce(edges, used, new Vec(s.e1.to, s.e1.from, s.e1.length)));
                            max = Math.max(max, bruteForce(edges, used, new Vec(s.e2.to, s.e2.from, s.e2.length)));
                        }
                        used.remove(j);
                    }
                used.remove(i);
            }
        return max;
    }

    static double bruteForce(double [] edges) {
        Set<Integer> used = new HashSet<>();
        double max = 0.0;
        for(int i = 0; i < edges.length; i  ) {
            used.add(i);
            max = Math.max(max, bruteForce(edges, used, new Vec(new V2(0.0, 0.0), new V2(0.0, edges[i]), edges[i])));
            used.remove(i);
        }
        return max;
    }

    public static void main(String... args) {
        double r = bruteForce(new double [] {42, 40, 32, 30, 25, 18, 15});
        System.out.println("    "   r   " (err: "   Math.abs(66.9495287 - r)   ")");
}

with output

66.94952872219118 (err: 2.2191173343344417E-8)

instead of brute force, we can use a simple heuristic, which is that, as each triangle needs two edges, from the point where we are we can advance, at most, the sum of the outstanding edges divided by two, if it is not enough, it is not worth to continue

static double heuristic(double best, double [] edges, Set<Integer> used, Vec base) {
    if(edges.length - used.size() < 2)
        return 0.0;
    double max = best;
    // for every two (not used) edges we can construct a new triangle
    for(int i = 0; i < edges.length; i  )
        if(!used.contains(i)) {
            used.add(i);
            for (int j = 0; j < edges.length; j  )
                if(!used.contains(j)) {
                    used.add(j);
                    Step s = next(base, edges[i], edges[j]);
                    if(s != null) {
                        // if not enough edges to reatch the best don't try
                        double maxNext = 0.0;
                        for(int k = 0; k < edges.length; k  )
                            if(!used.contains(k))
                                maxNext  = edges[k];
                        if(s.vertex.x > best - 0.5 * maxNext) {
                            max = Math.max(max, s.vertex.x);
                            max = Math.max(max, heuristic(max, edges, used, s.e1));
                            max = Math.max(max, heuristic(max, edges, used, s.e2));
                            max = Math.max(max, heuristic(max, edges, used, new Vec(s.e1.to, s.e1.from, s.e1.length)));
                            max = Math.max(max, heuristic(max, edges, used, new Vec(s.e2.to, s.e2.from, s.e2.length)));
                        }
                    }
                    used.remove(j);
                }
            used.remove(i);
        }
    return max;
}

static double heuristic(double [] edges) {
    Set<Integer> used = new HashSet<>();
    double max = 0.0;
    for(int i = 0; i < edges.length; i  ) {
        used.add(i);
        max = Math.max(max, heuristic(max, edges, used, new Vec(new V2(0.0, 0.0), new V2(0.0, edges[i]), edges[i])));
        used.remove(i);
    }
    return max;
}

to obtain the best possible algorithm, apply the same heuristic but add each state in a priority queue, so you will always take the step that has the best chance to advance and therefore eliminate candidates.