Questions:

Given a directed graph of N nodes and M edges (M <= 2.N). Find all the nodes that is reachable from all other nodes.

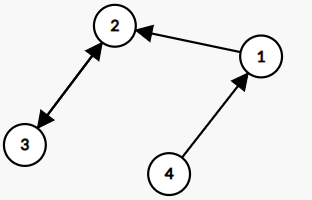
Example:

The below graph has 4 nodes and 4 edges:

Answer: Node (2) and (3) is reachable from all other nodes.

P/S:

The only solution I came up with is to revert the graph, BFS all nodes and check if they reach all other nodes. But it would take O(n^2).

Is there any other approach that takes O(n.logn) or less?

Here's my take on the O(n^2) approach:

void init(){
    cin >> n >> m;
    for(int i = 0; i < m; i  ){
        int u, v; cin >> u >> v;
        adj[v].emplace_back(u);
    }
}

void dfs(int u){
    visited[u] = true;
    for(int v : adj[u])
        if(!visited[v]) dfs(v);
}

init();
for(int u = 1; u <= n; u  ){
    memset(visited, 0, sizeof visited);
    dfs(u);
    if(count(visited   1, visited   n   1, 1) == n) cout << u << ' ';
}

CodePudding user response：

Can You share that code which take O(n^2) ?

Anyway, This approach only take O(n), Which is better then O(n log n)!

class DirectedGraph {
    graph = {}
    constructor(directedGraph) {
        for (let [id, arrow] of directedGraph)
            this.graph[id] = { arrow, isVisited: false }
    }
    find_end_points(id) {
        let out = [], graph = this.graph;
        function go_next(id, from) {
            let node = graph[id];
            if (node.isVisited || !node.arrow) return out.push(id)
            if (node.arrow == from) out.push(id);
            node.isVisited = true;
            go_next(node.arrow, id);
        }
        go_next(id, null);
        return out
    }
}
let directedGraph = new DirectedGraph([[2, 3], [3, 2], [1, 2], [4, 1]]);
console.log(directedGraph.find_end_points(4))

<iframe name="sif1" sandbox="allow-forms allow-modals allow-scripts" frameborder="0"></iframe>

CodePudding user response：

You can get an O(|V| |E|) algorithm using Tarjan's strongly connected components algorithm. Many sample implementations are available online or in standard algorithms textbooks.

Once you have the strongly connected components, the set of vertices reachable from all others is exactly the set of vertices whose strongly connected component(s) have out-degree 0 (the sinks in the graph). However, there is one exception: if the condensation of the graph (the new graph induced by the strongly connected components) is not connected, there are no such vertices. You can test the connectivity of a directed acyclic graph in O(|V|) time, by running a breadth-first search from any in-degree 0 vertex.