About np.einsum-CodePudding

I don't understand how the following code realizes the transformation of dimensions? The shape of C is [2, 3, 3, 4]. How to realize the following matrix operation without einsum function?

import numpy as np
a = np.random.randint(0, 10, (2,3,4))
b = np.random.randint(0, 10, (3, 6, 4))
c = np.einsum('bld,hid-> blhd', a,b)

CodePudding user response：

To answer your first question

c = np.einsum('bld,hid->blhd', a,b)

implements the formula

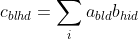
$c_{blhd} = \sum_{i} a_{bld} b_{hid}$

which, if you don't want to use einsum, you can achieve using

c = a[:, :, None, :] * b.sum(-2)[None, None, :, :]
#     b  l  (h)   d    i         (b)   (l)   h  d

CodePudding user response：

You can find more details in about einstein notation wikipedia

This means that you have indices b,l,h,i,d this will iterate the indices to cover all the inputs and build the input

I will use capital letters for the arrays here to distinguish from the indices.

C[b,l,h,d]  = A[b,l,d] * B[h,i,d]

The shape of the output can be determined as follows. You take the index of each output axis and look for the same index in the input. For instance the first axis of C is indexed with b that is also used to index the first axis of A, thus assert C.shape[0] == A.shape[0]. Repeating for the other axes we have assert C.shape[1] == A.shape[1], assert C.shape[2] == B.shape[0], and assert C.shape[3] == A.shape[2], also assert C.shape[3] == B.shape[2].

Notice that the index i does not affect where the term will be added, each element of the output can be written as

C[b,l,h,d] = sum(A[b,l,d] * B[h,i,d] for i in range(B.shape[1]))

Notice also that i is not used to index A. So this could be also written as

C[b,l,h,d] = A[b,l,d] * B[h,:,d].sum();

Or if you want to use vectorized operation

first expanding then reducing

C = A[:,:,None,:] * B[None,None,:,:,:].sum(-2)

expanding reducing then expandin, possible because A does not use i

C = A[:,:,None,:] * B.sum(-2)[None,None,:,:]