I am having an issue creating an example ODE given in Matlab to work with scipy's solve_ivp. In Matlab, the function is defined as

function fixed_point_linear_center()
    clc; clf;

    stepsize=.5;
    xmin=-5;
    xmax=5;
    ymin=-5;
    ymax=5;

    [x,y] = meshgrid(xmin:stepsize:xmax,ymin:stepsize:ymax);

    A = [0 1;-1 0];

    dx = A(1,1)*x   A(1,2)*y;
    dy = A(2,1)*x   A(2,2)*y;

    % Strange scaling for nicer output, only "cosmetics"
    eunorm = ( dx.^2   dy.^2 ).^(0.35);
    dx = dx./eunorm;
    dy = dy./eunorm;

    quiver(x,y,dx,dy);
    axis([xmin xmax ymin ymax]);
    grid on; xlabel('x'); ylabel('y');

    tspan=[0 100];

    x0stepsize=0.25;
    for x0=xmin:x0stepsize:xmax
        hold on
        ic = [x0 0];
        [~,x] = ode45(@(t,x) f(t,x,A),tspan,ic);
        plot(x(:,1),x(:,2),'r');
        hold on
        ic = [0 x0];
        [~,x] = ode45(@(t,x) f(t,x,A),tspan,ic);
        plot(x(:,1),x(:,2),'r');
    end
    hold off
end

function dx = f(~,x,A)
    dx = A*[x(1); x(2)];
end

to calculate the solution which looks like this

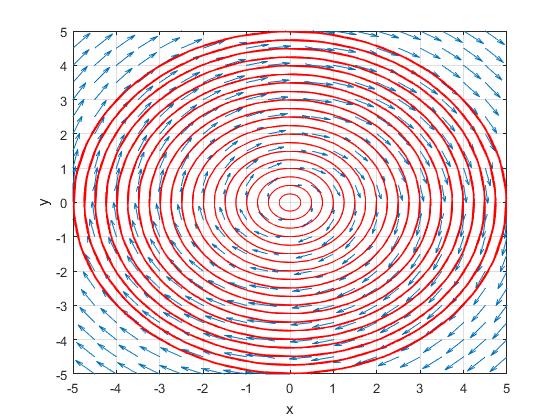
, however if I recreate the functions in python like this

def fixed_point_linear_center():
    stepsize   =  0.5
    x0stepsize =  0.25
    xmin       = -5
    xmax       =  5
    ymin       = -5
    ymax       =  5
    
    x    = np.arange(xmin, xmax stepsize, stepsize)
    xval = np.arange(xmin, xmax x0stepsize, x0stepsize)
    y    = np.arange(ymin, ymax stepsize, stepsize)
    yval = np.arange(ymin, ymax stepsize*0.25, stepsize*0.25) # evaluate 4 times for smoothness
    
    [X, Y] = np.meshgrid(x, y)
    
    
    A = np.array([[0,1],[-1,0]])

    dx = A[0,0]*X   A[0,1]*Y # 21x21
    dy = A[1,0]*X   A[1,1]*Y # 21x21
    
    f = lambda t,x,A : np.dot(A,[[x[0]],[x[1]]])

    # Strange scaling for nicer output, but only "cosmetics"
    eunorm = np.float_power(( dx**2   dy**2 ), 0.35)   #( dx**2   dy**2 )**0.35
    eunorm[10,10] = 0.001 # center is 0 which violates division
    dx = dx/eunorm
    dy = dy/eunorm

    plt.figure(figsize = (15,12))
    plt.quiver(X, Y, dx, dy, angles = 'xy', color='#0086b3', width=0.0015)
    plt.grid() 
    plt.xlabel('x') 
    plt.ylabel('y')

    plt.axis([xmin,xmax,ymin,ymax])
    
    tspan=[0,100]
    
    for x0 in xval:
        
        ic = [x0,0]
        #[~,x] = ode45(@(t,x) f(t,x,A),tspan,ic);
        solution = solve_ivp(f, [xmin, xmax], ic, method='RK45', t_eval=yval, dense_output=True, args=(A,))
        #solution = solve_ivp(f, [xmin, xmax], [x0], method='RK45', t_eval=yval, dense_output=False, args=(0,A))
        #solution = solve_ivp(f, [tmin, tmax], [ic], method='RK45', t_eval=tval, args=(A), dense_output=False)
        plt.plot(solution.y[1], solution.y[0],'r')
        
fixed_point_linear_center()

I get errors like

ValueError: shapes (2,2) and (2,1,2) not aligned: 2 (dim 1) != 1 (dim 1)

or similar, depending on what I already tried to rewrite f to. As I understand, solve_ivp expects a single value in the x0 array, while I return a 2x1 vector. It also doesn't accept a vector as value in it's x0 array like [[x0,0]]

Now I wonder if scipy.solve_ivp able to do the calculation like ode45 for parameter space (and how do I do it) or do I have to do the calculation otherwise?

(I checked already, that all other matrices and return values are identical with the matlab calculation.)

[EDIT 2] okay, it works now. The plot parameter for x had to be solution.y[1] of course!

CodePudding user response：

Just like the Matlab solver, solve_ivp expects the state to be a single vector. Change

f = lambda t,x1,x2, A : np.dot(A,[[x1],[x2]])

to

f = lambda t, x, A : np.dot(A, x)

Also, to ensure ensure that solve_ivp interprets the shape of the argument A correctly, pass it to solve_ivp with args=(A,) (note the use of the comma).