I am trying to apply the idea of sklearn 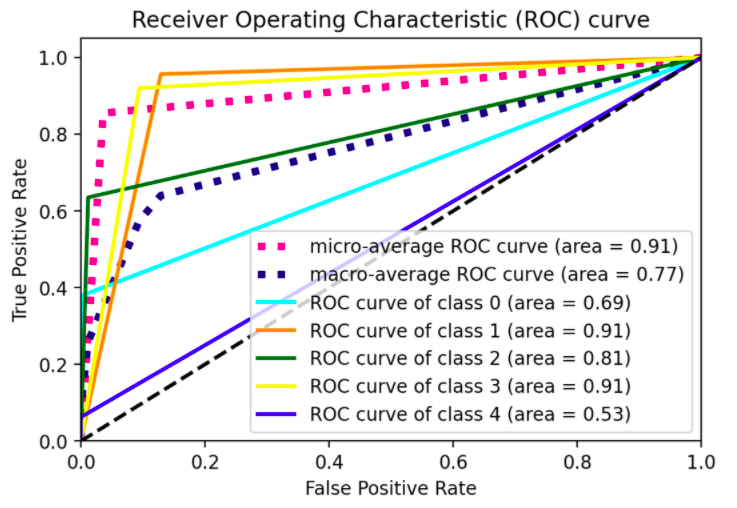
Kind of straight line bending once. I would like to see the model performance at different thresholds, not just one, a figure similar to 
CodePudding user response:
Point is that you're using
predict()rather thanpredict_proba()/decision_function()to define youry_hat. This means - considering that the threshold vector is defined by the number of distinct values iny_hat(see here for reference), that you'll have few thresholds per class only on whichtprandfprare computed (which in turn implies that your curves are evaluated at few points only).Indeed, consider what the doc says to pass to
y_scoresinroc_curve(), either prob estimates or decision values. In the example fromsklearn, decision values are used to compute the scores. Given that you're considering aRandomForestClassifier(), considering probability estimates in youry_hatshould be the way to go.What's the point then of label-binarizing the output? The standard definition for ROC is in terms of binary classification. To pass to a multiclass problem, you have to convert your problem into binary by using OneVsAll approach, so that you'll have
n_classnumber of ROC curves. (Observe, indeed, that asSVC()handles multiclass problems in a OvO fashion by default, in the example they had to force to use OvA by applyingOneVsRestClassifierconstructor; with aRandomForestClassifieryou don't have such problem as that's inherently multiclass, see here for reference). In these terms, once you switch topredict_proba()you'll see there's no much sense in label binarizing predictions.# all imports import numpy as np import matplotlib.pyplot as plt from itertools import cycle from sklearn import svm, datasets from sklearn.metrics import roc_curve, auc from sklearn.model_selection import train_test_split from sklearn.preprocessing import label_binarize from sklearn.datasets import make_classification from sklearn.ensemble import RandomForestClassifier # dummy dataset X, y = make_classification(10000, n_classes=5, n_informative=10, weights=[.04, .4, .12, .5, .04]) train, test, ytrain, ytest = train_test_split(X, y, test_size=.3, random_state=42) # random forest model model = RandomForestClassifier() model.fit(train, ytrain) yhat = model.predict_proba(test) def plot_roc_curve(y_test, y_pred): n_classes = len(np.unique(y_test)) y_test = label_binarize(y_test, classes=np.arange(n_classes)) # Compute ROC curve and ROC area for each class fpr = dict() tpr = dict() roc_auc = dict() thresholds = dict() for i in range(n_classes): fpr[i], tpr[i], thresholds[i] = roc_curve(y_test[:, i], y_pred[:, i], drop_intermediate=False) roc_auc[i] = auc(fpr[i], tpr[i]) # Compute micro-average ROC curve and ROC area fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_pred.ravel()) roc_auc["micro"] = auc(fpr["micro"], tpr["micro"]) # First aggregate all false positive rates all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)])) # Then interpolate all ROC curves at this points mean_tpr = np.zeros_like(all_fpr) for i in range(n_classes): mean_tpr = np.interp(all_fpr, fpr[i], tpr[i]) # Finally average it and compute AUC mean_tpr /= n_classes fpr["macro"] = all_fpr tpr["macro"] = mean_tpr roc_auc["macro"] = auc(fpr["macro"], tpr["macro"]) # Plot all ROC curves #plt.figure(figsize=(10,5)) plt.figure(dpi=600) lw = 2 plt.plot(fpr["micro"], tpr["micro"], label="micro-average ROC curve (area = {0:0.2f})".format(roc_auc["micro"]), color="deeppink", linestyle=":", linewidth=4,) plt.plot(fpr["macro"], tpr["macro"], label="macro-average ROC curve (area = {0:0.2f})".format(roc_auc["macro"]), color="navy", linestyle=":", linewidth=4,) colors = cycle(["aqua", "darkorange", "darkgreen", "yellow", "blue"]) for i, color in zip(range(n_classes), colors): plt.plot(fpr[i], tpr[i], color=color, lw=lw, label="ROC curve of class {0} (area = {1:0.2f})".format(i, roc_auc[i]),) plt.plot([0, 1], [0, 1], "k--", lw=lw) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel("False Positive Rate") plt.ylabel("True Positive Rate") plt.title("Receiver Operating Characteristic (ROC) curve") plt.legend()
Eventually, consider that roc_curve() has also a drop_intermediate parameter meant for dropping suboptimal thresholds (it might be useful to know).
