Is there a clever way to determine the points that are inside of an arbitrary shape?-CodePudding

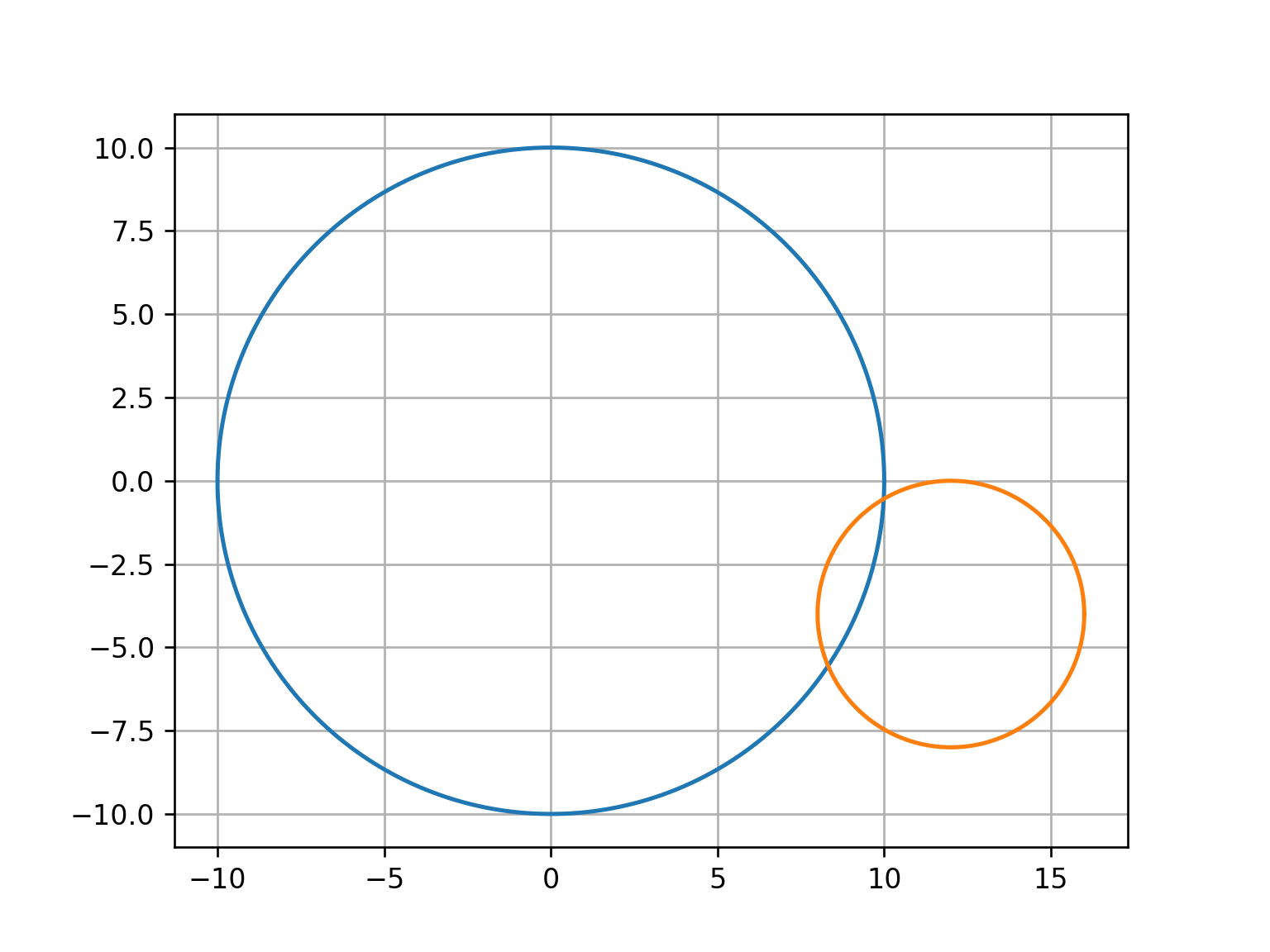
My goal is to determine if points lie inside of a shape. Consider the following example:

import numpy as np
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings('ignore', 'invalid value encountered in sqrt')

r1 = 10
r2 = 4
a = 12  # x shift for circle 2
b = -4  # y shift for circle 2

theta = np.arange(0, 2*np.pi, 0.0006)

r1_complex = r1*np.exp(1j*theta)
r1_x, r1_y = np.real(r1_complex), np.imag(r1_complex)

r2_complex = r2*np.exp(1j*theta)
r2_x, r2_y = np.real(r2_complex)   a, np.imag(r2_complex)   b

fig, ax = plt.subplots()

ax.plot(r1_x, r1_y)
ax.plot(r2_x, r2_y)

ax.set_aspect('equal')
ax.grid()
plt.show()

output

I want to find the points of the blue circle that are inside of the orange circle. It would be best to try and find it without iteration if possible.

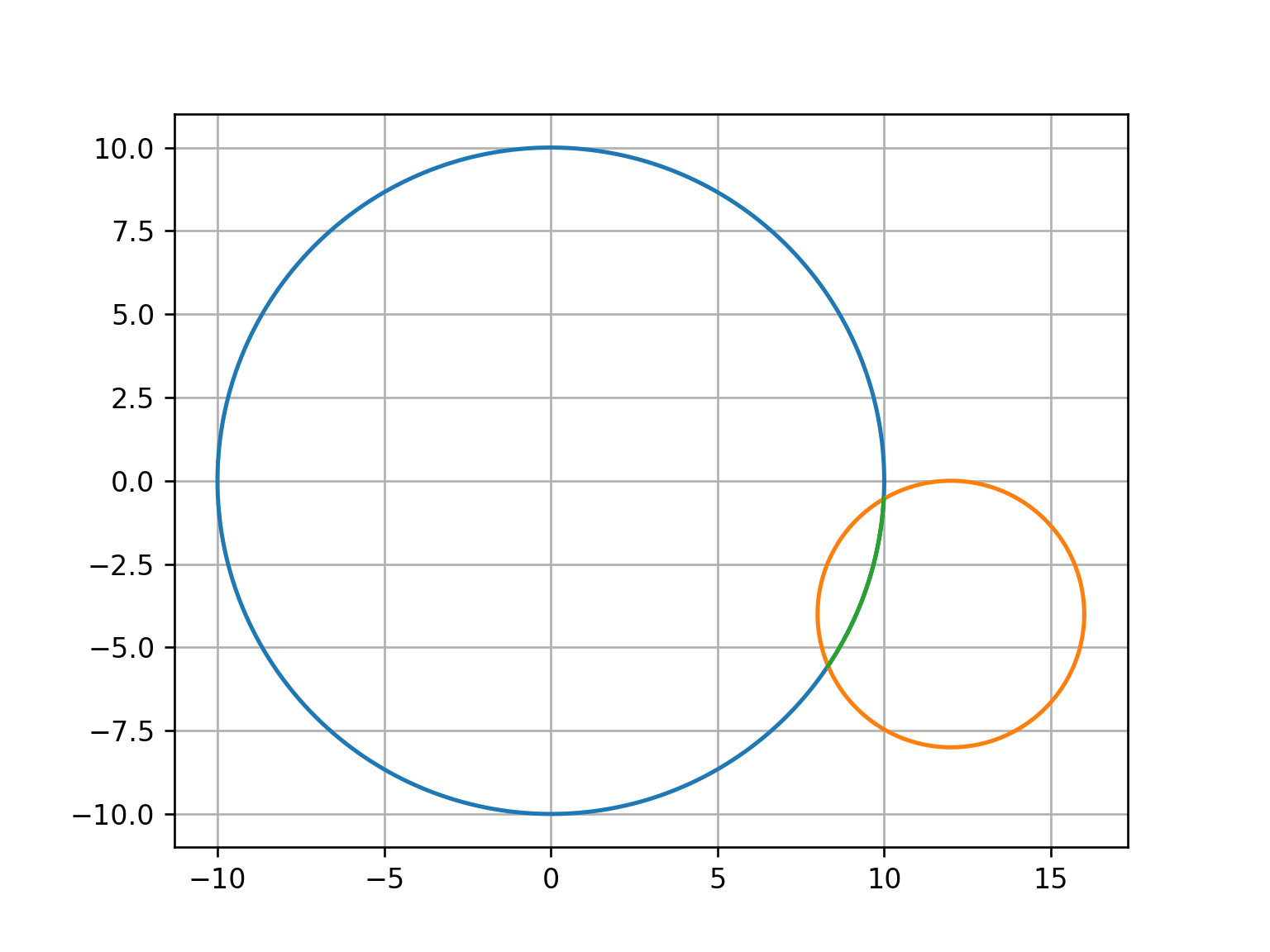
For this case, I can easily determine the points that are inside of the orange circle because I know the equation of a circle. Amending the code to this:

import numpy as np
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings('ignore', 'invalid value encountered in sqrt')

r1 = 10
r2 = 4
a = 12  # x shift for circle 2
b = -4  # y shift for circle 2

theta = np.arange(0, 2*np.pi, 0.0006)

r1_complex = r1*np.exp(1j*theta)
r1_x, r1_y = np.real(r1_complex), np.imag(r1_complex)

r1_inside_y = np.logical_and(r1_y < np.sqrt(r2**2 - (r1_x - a)**2)   b, r1_y > -np.sqrt(r2**2 - (r1_x - a)**2)   b)

r2_complex = r2*np.exp(1j*theta)
r2_x, r2_y = np.real(r2_complex)   a, np.imag(r2_complex)   b

fig, ax = plt.subplots()

ax.plot(r1_x, r1_y)
ax.plot(r2_x, r2_y)
ax.plot(r1_x[r1_inside_y], r1_y[r1_inside_y])

ax.set_aspect('equal')
ax.grid()
plt.show()

output

produces what I'm looking for. Is there a way to get this same result without knowing the equation for a circle? Perhaps an algorithm, or clever way with numpy operations?

edit

What I mean by arbitrary shape is an kind of closed shape with N number of points. Consider this image:

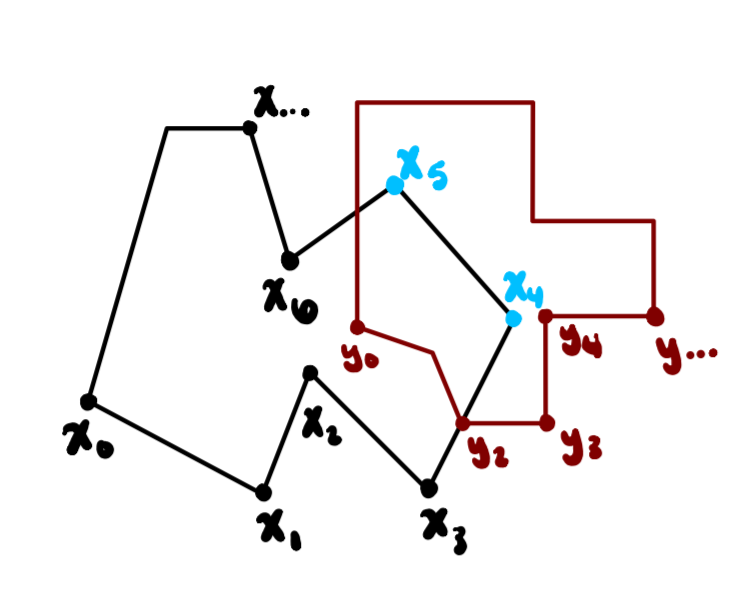
I would like to know the points from the black line that lie inside the bounds of the red line. For this example, there are two points that this algorithm should find, the x4 and x5 points in blue. And the points x1, x2, ... xN would be coordinate points where both shapes share the same origin.

CodePudding user response：

It turns out, this algorithm has already been standardized in the matplotlib.path module. You can produce the same results using the Path class. Consider the following changes to the above code:

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import path

r1 = 10
r2 = 4
a = 12  # x shift for circle 2
b = -4  # y shift for circle 2

theta = np.arange(0, 2*np.pi, 0.0006)

r1_complex = r1*np.exp(1j*theta)
r1_x, r1_y = np.real(r1_complex), np.imag(r1_complex)
stacked1 = np.stack((r1_x, r1_y), axis=1)  # A list of coordinates

r2_complex = r2*np.exp(1j*theta)
r2_x, r2_y = np.real(r2_complex)   a, np.imag(r2_complex)   b
stacked2 = np.stack((r2_x, r2_y), axis=1)  # A list of coordinates

p = path.Path(stacked2)
r1_inside = p.contains_points(stacked1)

fig, ax = plt.subplots()

ax.plot(r1_x, r1_y)
ax.plot(r2_x, r2_y)
ax.plot(r1_x[r1_inside], r1_y[r1_inside])

ax.set_aspect('equal')
ax.grid()
plt.show()

This produces the same image without knowledge of the mathematical properties of the shapes.