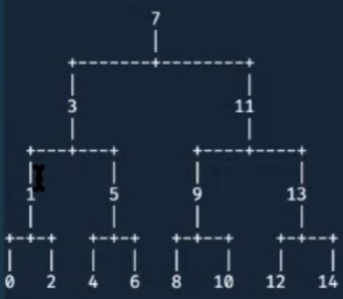
I created a binary search tree and tried to print the binary search tree with this instance
data Tree a = Nil | Node (Tree a) a (Tree a)
instance Show a => Show (Tree a) where
show t = intercalate "\n" (map snd (draw t))
draw :: Show a => Tree a -> [(Int,String)]
draw Nil = [(1,"*")]
draw (Node Nil x Nil) = [(1,show x)]
draw (Node tl x tr) = zip (repeat 0) (map shiftl (draw tl)) [(1,show x "- ")] zip (repeat 2) (map shiftr (draw tr)) where
shiftl (0,x) = spaces " " x
shiftl (1,x) = spaces " -" x
shiftl (2,x) = spaces "| " x
shiftr (0,x) = spaces "| " x
shiftr (1,x) = spaces " -" x
shiftr (2,x) = spaces " " x
spaces = replicate (length (show x) 1) ' '
createTree :: [a] -> BTree a
createTree [] = Nil
createTree xs = Node
(createTree front) x (createTree back) where
n = length xs
(front, x:back) = splitAt (n `div` 2) xs
Now I want to print it horizontally, which i am not able to do so. I want to print the binary search tree like this picture below. (Sorry for the low quality of the picture but you get the idea). How can i do it ?
Use the sample example [1..50]
UPDATE ANSWER :-
I found my answer myself. I created one function that shows like that. The code is in the comments.
If you have an other solution please share
CodePudding user response:
I found my answer myself. I created one function that shows like that. Here is the code
import Data.List (intercalate)
data BTree a = Nil | Node (BTree a) a (BTree a) deriving Eq
-- Instances of BST
instance Show a => Show (BTree a) where
show t = "\n" intercalate "\n" (map (map snd) (fst $ draw5 t)) "\n"
-- End of instances
data Tag = L | M | R deriving (Eq,Show)
type Entry = (Tag, Char)
type Line = [Entry]
--the tag thing is for my own understanding that do no work here.
createTree :: [a] -> BTree a
createTree [] = Nil
createTree xs = Node
(createTree front) x (createTree back) where
n = length xs
(front, x:back) = splitAt (n `div` 2) xs
-- my own draw
draw5 :: Show a => BTree a -> ([Line],(Int,Int,Int))
draw5 Nil = ([zip [M] "*"],(0,1,0) )
draw5 (Node Nil x Nil) =
let (sx,n,m) = (show x, length sx, n `div` 2) in
([zip (replicate m L [M] replicate (n-m-1) R) sx], (m,1,n-m-1))
draw5 (Node tl x tr) = (l1:l2:l3:l4:mainline,(a,b,c)) where
(mainline ,(a,b,c)) = drawing xs ys
(xs,(xsa,xsb,xsc)) = draw5 tl
(ys,(ysa,ysb,ysc)) = draw5 tr
drawing xs ys = (join xs ys, (xsa xsb xsc 1, 1, ysa ysb ysc 1) )
join (as:ass) (bs:bss) = go as bs : join ass bss
join xss [] = map ( ([(L,' '),(M, ' '),(R,' ')] replicate (ysa ysb ysc) (R,' ') )) xss
join [] yss = map ((replicate (xsa xsb xsc) (L,' ') [(L,' '),(M, ' '),(R,' ')]) ) yss
go xss yss = xss [(L,' '),(M, ' '),(R,' ')] yss
([cs],(m,n,o)) = draw5 (Node Nil x Nil)
l1 = replicate (a-m) (L,' ') cs replicate (c-o) (R,' ')
l2 = replicate a (L,' ') [(M, '|')] replicate c (R,' ')
l3 = replicate xsa (L,' ') [(L,' ')] replicate (xsc 1) (L,'-') [(M,' ')] replicate (ysa 1) (R,'-') [(R,' ')] replicate ysc (R,' ')
l4 = replicate xsa (L,' ') [(L,'|')] replicate (xsc ysa 3) (M,' ') [(R,'|')] replicate ysc (R,' ')
CodePudding user response:
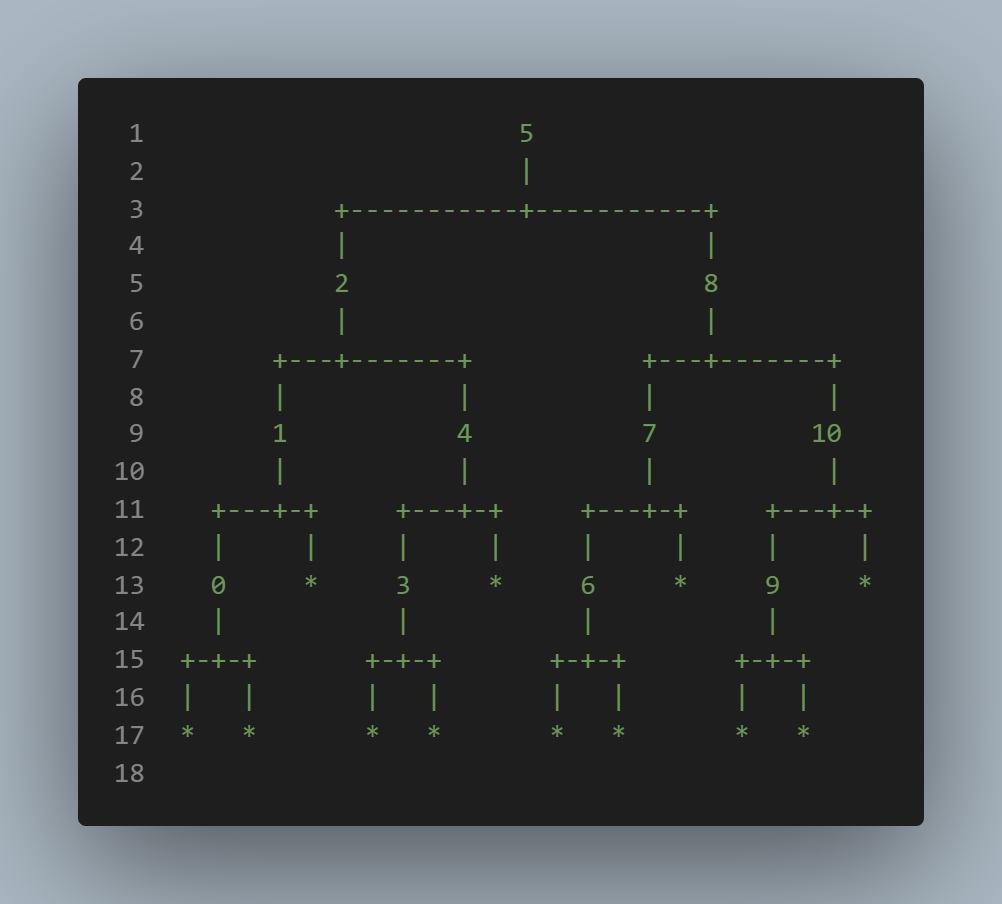
Here's my solution. It's not perfect. It assumes that values has at most 3 digits. It also prints Nil nodes as a *.
The basic idea is to first get the visualizations of the left and right trees as two lists of strings. Then they are zipped using concatenation to produce a list of strings representing the two trees side-by-side.
myShow :: Show a => Tree a -> [Char]
myShow tree =
let (s, _, _) = show' tree
in intercalate "\n" s
where
show' :: Show a => Tree a -> ([String], Int, Int)
show' Nil = (["*"], 1, 0)
show' (Node ltree value rtree) = (ashow, awidth, acenter)
where
centerAtColumn :: String -> Int -> Int -> String
centerAtColumn string width column =
let
whitespaceWidth = width - length string
leftPadding = whitespaceWidth `div` 2
rightPadding = whitespaceWidth - leftPadding
in
replicate leftPadding ' ' string replicate rightPadding ' '
middle_padding_length = 1
middle_padding = replicate (2*middle_padding_length 1) ' '
(lshow, lwidth, lcenter) = show' ltree
(rshow, rwidth, rcenter) = show' rtree
awidth = lwidth length middle_padding rwidth
acenter = lwidth middle_padding_length
-- Put subtrees side by side with some padding
ldepth = length lshow
rdepth = length rshow
sdepth = max ldepth rdepth
sshow = take sdepth $
zipWith (\s1 s2 -> s1 middle_padding s2)
(lshow replicate (sdepth-ldepth) (replicate lwidth ' '))
(rshow replicate (sdepth-rdepth) (replicate rwidth ' '))
wshow = map (\s -> s replicate (awidth - length s) ' ') sshow
vshow =
replicate lcenter ' ' [' '] replicate (lwidth-lcenter-1) ' '
centerAtColumn (show value) (length middle_padding) middle_padding_length
replicate rcenter ' ' [' '] replicate (rwidth-rcenter-1) ' '
position :: [Char] -> String
position [c1, c2, c3, c4, c5, c6, c7] =
replicate lcenter c1 [c2] replicate (lwidth-lcenter-1) c3
[ c3, c4, c5 ]
replicate rcenter c5 [c6] replicate (rwidth-rcenter-1) c7
position _ = error "position called with list with wrong count of elements"
pipes = position " | | "
splitter = position " - - "
ashow = vshow : (replicate lwidth ' ' " | " replicate rwidth ' ') : splitter : pipes : wshow
Output for createTree [0..10]: