How to get a smoothed contour line in matplotlib given non-smooth underlying data-CodePudding

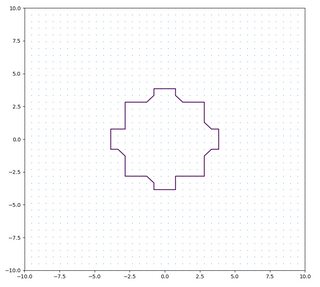
I have boolean data on a 2D grid and want to use matplotlib to plot a countour between the areas where the data is True and False.

However, the separation between these areas is not smooth within the actual data. How can I compute a smoothed countour given this data?

Here is a minimal example:

import numpy as np
import matplotlib.pyplot as plt

# generate some non-smooth example data
MESHSIZE = 10
REFINEMENT = 4*MESHSIZE
x = np.linspace(-MESHSIZE, MESHSIZE, REFINEMENT)
xv, yv = np.meshgrid(x, x)
xvf = xv.reshape(-1)
yvf = yv.reshape(-1)


def choppy_circle(x, y):
    inner = x.astype(int)**2 y.astype(int)**2 < 10.0
    return inner


# consider this the *actual* data given to me as-is
my_x = xvf
my_y = yvf
my_z = choppy_circle(xvf, yvf)

# need to visualize the contour that separates areas where
# my_z is True/False
plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))
plt.scatter(xv, yv, s=0.1)
plt.show()

This produces the following plot, which is faithful to the data, but not what I'm looking for:

How can I use the data given in my_x, my_y and my_z to construct a smoothed contour around the domain where my_z is True?

Something like this:

CodePudding user response：

You can fit a spline to the contour. And make it as smooth as you want by picking the spline's smoothing parameter.

First you obtain the boundary points

import functools
import itertools

mask = my_z.reshape(40,40)
mask &= functools.reduce(np.logical_or,[~np.roll(np.roll(mask, shift_x, 0),shift_y,1) 
                                            for shift_x,shift_y in itertools.product((-1,0,1),repeat=2)])
x,y = my_x[mask.reshape(-1)],my_y[mask.reshape(-1)]
plt.scatter(x,y)

Now we sort your points by the argument of the corresponding complex number. If you don't know what I mean by that it's the angle the point makes with the origin and the point (1,0). And fit a spline to it.

import scipy.interpolate as interpolate
import matplotlib.pyplot as plt

arr = np.array(sorted(zip(x,y), key=lambda x: cmath.phase(x[0] 1j*x[1])))
s=1

tck, u = interpolate.splprep([arr[:,0],arr[:,1]],per=1, s=s)
x_i, y_i = interpolate.splev(np.linspace(0, 1, 10**4), tck)
ax = plt.gca()
ax.plot(x_i, y_i)
ax.scatter(arr[:,0],arr[:,1])
ax.set_title(f"{s=}")
ax.set_aspect('equal')

The results look differently depending on s. I plotted it for a few for you:

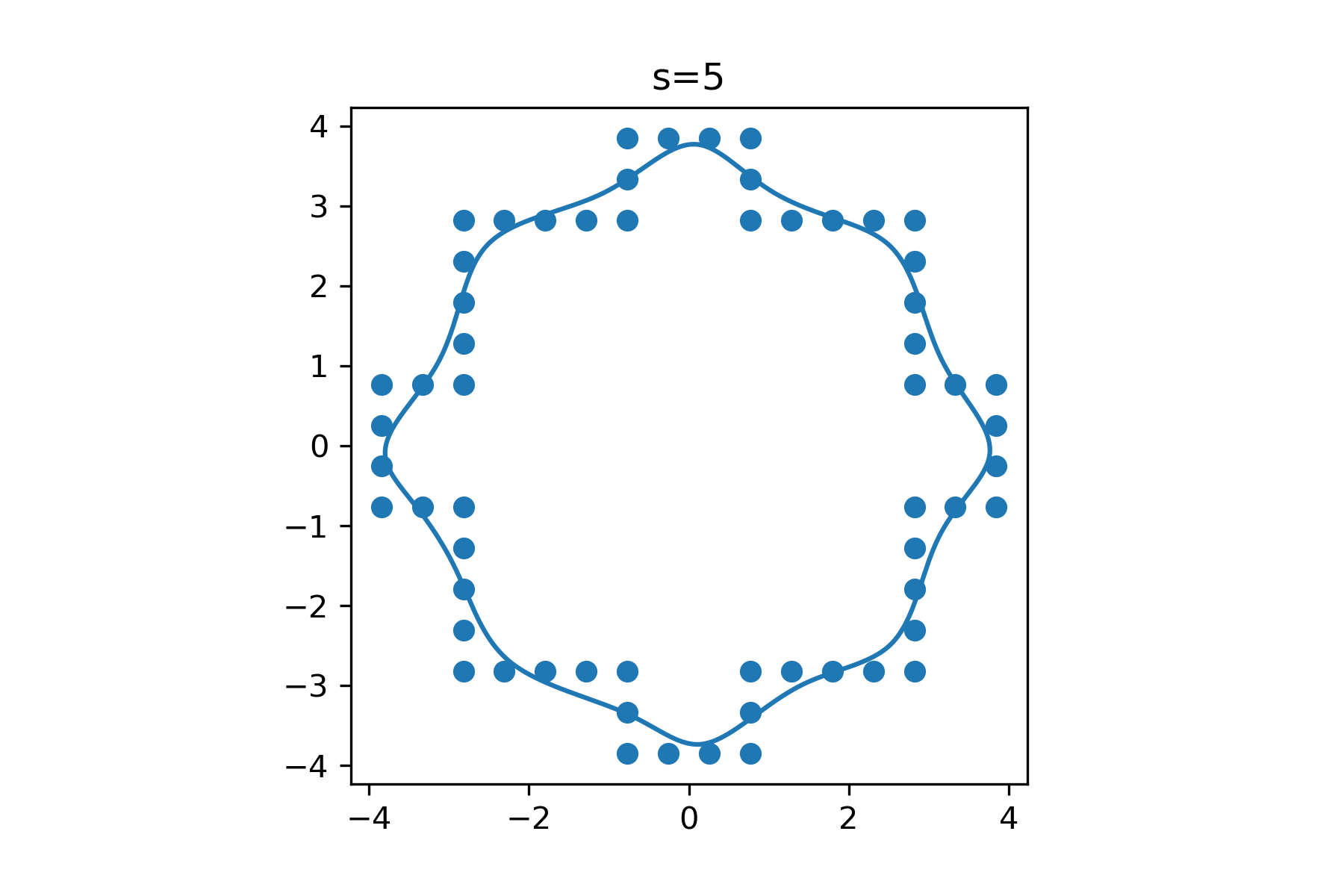
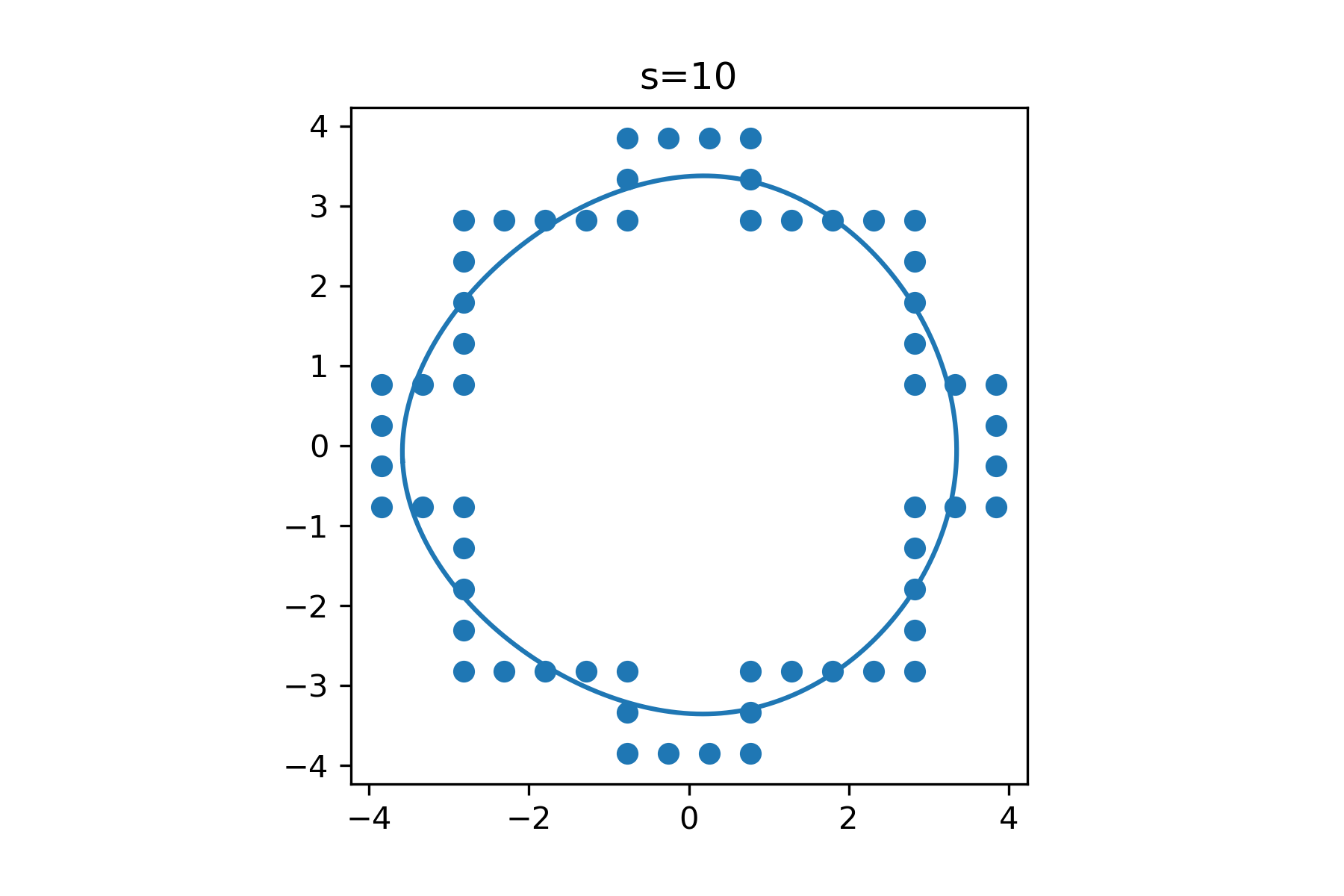
CodePudding user response：

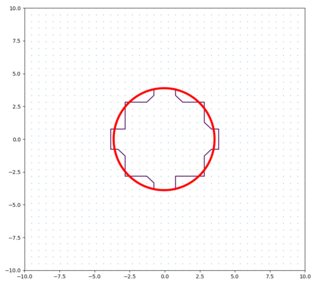
You can use shapely to get the centroid and bounding box of your arbitrary shape, then plot a circle:

# […] same as previously

# get points
cs = plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))
v = cs.collections[0].get_paths()[0].vertices

from shapely.geometry import Polygon

# find centroid coordinates and bounding box
p = Polygon(v)
x,y =p.centroid.coords[0]
minx, miny, maxx, maxy = p.bounds

# plot circle
# depending on the data, one could also plot an ellipse or rectangle
r = max((maxx-minx)/2, (maxy-miny)/2)
circle = plt.Circle((x, y), r, color='r', fill=False)
plt.gca().add_patch(circle)

output: