How to create a unit vector of AB towards a number of degrees and calculate the angle between them?-CodePudding

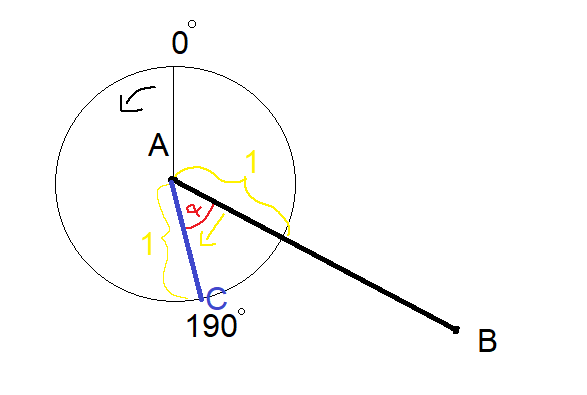
Here you can see the Vector AB.

Goal: Make Vector AC to find out α

Problem: To find out the angle α I would first need a second vector AC that must point towards 190° and has the same length as the unit vector of AB. How do I create that Vector?

            A = (5, 10)
            B = (10, 5)

            distance = np.array([B[0] - A[0], A[1] - B[1]]) # Vector from A to B
            unit_vector = distance / np.linalg.norm(distance) # unit vector

            # Need to make Vector AC here

            # Get angle between vector AB and vector AC
            AB = unit_vector(unit_vector)
            AC = unit_vector(c)
            print(np.arccos(np.clip(np.dot(AB, AC), -1.0, 1.0)))

CodePudding user response：

OK, look at this. Given your points (5,10) and (10,5):

C:\tmp>python
Python 3.7.3 (v3.7.3:ef4ec6ed12, Mar 25 2019, 22:22:05) [MSC v.1916 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> import math

## Find the angle to AB using traditional 0-to-the-right axes.

>>> math.atan2(-5,5)
-0.7853981633974483

## Convert to degrees.

>>> math.atan2(-5,5) * 180 / math.pi
-45.0

## Subtract 90 to shift the 0 point to the north

>>> math.atan2(-5,5) * 180 / math.pi - 90
-135.0

## Modulo 360 to make it positive

>>> (math.atan2(-5,5) * 180 / math.pi - 90) % 360
225.0

##  Subtract 190, and we get the value for the angle alpha.

>>> (math.atan2(-5,5) * 180 / math.pi - 90) % 360 - 190
35.0