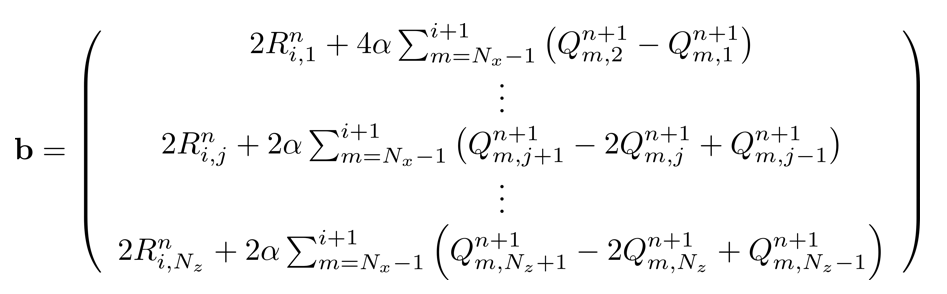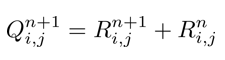Code performance optimization : speeding up population of an array in Matlab-CodePudding

Part of a longer algorithm, populating the column array b takes 80% of the total run time. The line (see code below) where S1 is calculated in the for loop is the bottleneck because it's called an enormously large amount of times due to the nested loops. I have tried vectorizing the loops and/or using the sum built-in function but I always end up with an even higher computation time.

For the sake of simplicity we can look at one single iteration, namely n = 1 and n 1 = 2. So the 3D array containing the quantity R at each iteration has only two elements : R(:,:,1) and R(:,:,2).

Where:

I have posted here a minimum working sample that you can yourself run:

tic

Nz = 3636 ;  % Number of rows 
Nx = 910 ;   % Number of columns

R = rand(Nz, Nx, 2) ;
alpha = 3 ;

  for ii = Nx - 1 : -1 : 2                
     b = zeros(Nz, 1) ;

     for jj = 2 : Nz - 1 
        S  = 0 ;
        S1 = 0 ;
          
         for mm = Nx - 1 : -1 : ii  % Summation 
             S1 = S1   R(2, mm, 2)   R(2, mm, 1) - (R(1, mm, 2)   R(1, mm, 1)) ; 
             S  = S   (R(jj   1, mm, 2)   R(jj   1, mm, 1)) - 2 * (R(jj, mm, 2)   R(jj, mm, 1))   (R(jj - 1 , mm, 2)   R(jj - 1, mm, 1)) ; 
              
         end

        b(1)  =  2 *(R(1, ii, 1)   2 * alpha * S1) ;       
        b(jj) =  2 *(R(jj, ii, 1)   alpha * S) ;
     end
 end
toc

The current elapsed time is about 28-30 [s] on my laptop (i7-9850H, 2.6 GHz, 16 GB RAM).

I am aware that b is reset to zero at each ii iteration, but to reduce the sample to bare minimum I omitted a line just before the last end: q = D\b. It's a linear system solved column by column starting from the right-most column of the grid (most external loop). That's why at every ii (column) iteration I compute a new b and thus a new solution q.

How can I speed up this computation?

EDIT:

I tried to vectorize the sum, by eliminating the inner for loop and using the function sum, but the time increases dramatically.

tic

Nz = 3636 ;  % Number of rows 
Nx = 910 ;   % Number of columns

R = rand(Nz, Nx, 2) ;
alpha = 3 ;

  for ii = Nx - 1 : -1 : 2                
     b = zeros(Nz, 1) ;

     for jj = 2 : Nz - 1 
       
         S1 = sum([R(2, Nx - 1 : -1 : ii, 2), R(2, Nx - 1 : -1 : ii, 1), - R(1, Nx - 1 : -1 : ii, 2), R(1,Nx - 1 : -1 : ii, 1)]) ; 
         S  = sum([R(jj   1, Nx - 1 : -1 : ii, 2), R(jj   1, Nx - 1 : -1 : ii, 1), - 2 * R(jj, Nx - 1 : -1 : ii, 2), 2 * R(jj, Nx - 1 : -1 : ii, 1), R(jj - 1 , Nx - 1 : -1 : ii, 2), R(jj - 1, Nx - 1 : -1 : ii, 1)]) ; 
              
        b(1)  =  2 *(R(1, ii, 1)   2 * alpha * S1) ;       
        b(jj) =  2 *(R(jj, ii, 1)   alpha * S) ;
     end
 end
toc

CodePudding user response：

On my laptop (MATLAB R2020a, i7-5500U, 2.4 GHz, 8 GB RAM), your original code runs in about 45 s.

Elapsed time is 45.239229 seconds.

Your attempt using sum runs in about 191 s.

Elapsed time is 191.424418 seconds.

@Ander Biguri suggestion runs in about 174 s, which is faster, but not as fast as using for loops.

Elapsed time is 174.288989 seconds.

It appears that MATLAB built-in sum function runs slower than the for loop, as briefly discussed here. The array initialization b=zeros(Nz,1) is fast in newer versions of MATLAB (at least since R2019a), but you can initialize it differently if you are using an older version.

@Ander suggestions, however, are noteworthy and we can follow his suggestions, but use for loop for the summations:

tic

Nz = 3636 ;  % Number of rows 
Nx = 910 ;   % Number of columns

R = rand(Nz, Nx, 2) ;
alpha = 3 ;

for ii = Nx - 1 : -1 : 2                
    b = zeros(Nz, 1) ;
    S1 = 0 ;
    for mm = Nx - 1 : -1 : ii  % Summation 
        S  = S   (R(jj   1, mm, 2)   R(jj   1, mm, 1)) - 2 * (R(jj, mm, 2)   R(jj, mm, 1))   (R(jj - 1 , mm, 2)   R(jj - 1, mm, 1)) ; 
    end
         
    for jj = 2 : Nz - 1 
        S  = 0 ;

         for mm = Nx - 1 : -1 : ii  % Summation 
             S  = S   (R(jj   1, mm, 2)   R(jj   1, mm, 1)) - 2 * (R(jj, mm, 2)   R(jj, mm, 1))   (R(jj - 1 , mm, 2)   R(jj - 1, mm, 1)) ; 
         end

        b(1)  =  2 *(R(1, ii, 1)   2 * alpha * S1) ;       
        b(jj) =  2 *(R(jj, ii, 1)   alpha * S) ;
    end
end
toc

Elapsed time is 26.911663 seconds.

If computing time is a big concern, you can create some temporary variables before the for loop to avoid some summations/multiplications. This makes the code slightly worse to read, but it runs faster:

tic

Nz = 3636 ;  % Number of rows 
Nx = 910 ;   % Number of columns

R = rand(Nz, Nx, 2) ;
R12 = R(:,:,1) R(:,:,2);
alpha = 3 ;

Nx1 = Nx-1;
Nz1 = Nz-1;
two_alpha = 2*alpha;

for ii = Nx1:-1:2                
    b = zeros(Nz, 1) ;

    S1 = 0 ;
    for mm = ii:Nx1 % Summation 
        S1 = S1   R12(2, mm) - R12(1, mm) ; 
    end
    
    for jj = 2:Nz1
        S  = 0 ;
        for mm = ii:Nx1  % Summation 
            S  = S   R12(jj   1, mm) -2*R12(jj, mm)   R12(jj - 1 , mm) ; 
        end
        b(1)  =  2 *(R(1, ii,1)   two_alpha*S1) ;       
        b(jj) =  2 *(R(jj, ii,1)   alpha*S) ;
    end
end
toc

Elapsed time is 12.202103 seconds.

Since the limits of summation extend up to N-1, creation of the Nx1 and Nz1 variables avoids three subtractions on each ii-loop. The two_alpha variable also avoids one multiplication per iteration. Creation of the R12 also speeds up calculation, since in the original code this sum on the 3rd dimesion appears on every line of the summations.

I tried to also create a two_R12=2*R12 variable for the mm-loop, but it runs slower since the for loop must access elements on two different variables.

You also stated that the b variable is used to solve a liner system q = D\b. This will also slow down computations. If the D matrix is constant, consider decompose it, in order to also speed up calculations.

CodePudding user response：

Im jut working with your optimized code. Mostly because your optimized code does not do the same as the non optimized one, there are more things that make no sense (b is replaced in all of the ii loops, so ii is superfluous). I give you thus some tips to improve code in general, but can't fix a broken question.

Tips:

make your code easy to read by you. R(2, Nx - 1 : -1 : ii, 2), R(2, Nx - 1 : -1 : ii, 1) is just R(2, Nx - 1 : -1 : ii, 2:1), and in fact as you are adding them R(2, Nx - 1 : -1 : ii, :).
Indexing an array is much faster if you do it as expected, i.e. in order. You are adding array elements, but reading them in reverse. Just read them normally, i.e. Nx-1:-1:ii is just ii:Nx-1. Bonus that its much more readable. In fact the above line is no suddenly R(2, ii:Nx-1, :) much more readable.

Don't create temporary arrays if can be avoided. Particularly if in the end, these will be the size of R! You are just indexing it, and you dont care about the ordering because you will add it together. S can be just:

S  = sum(R(jj-1:jj 1, ii : Nx-1, :).*cat(3,[1;2;1],[1; -2; 1]),'all') ; 

% R(jj-1:jj 1, ii : Nx-1, :)   % grabs the needed values
% cat(3,[1;2;1],[1; -2; 1])    % small trick to multiply the arrays (implicit broadcast)
% sum(  ,'all')                % add them regarthless of shape.

This already speeds up the code by a lot.

4- Dont overcompute. S1 does not depend in jj, in fact, its the same for each ii. So why compute it jj times each ii ?

So, you can change your optimized code to the following for a x1.7 speedup:

tic


Nz = 1000 ;  % Number of rows
Nx = 200 ;   % Number of columns


R = rand(Nz, Nx, 2) ;
alpha = 3 ;

for ii = Nx - 1 : -1 : 2
    b1 = zeros(Nz, 1) ;
    
    % we can optimize this one too, but I don't think its the main culprit
    % here. 
    S1 = sum([R(2, ii : Nx-1, 2), R(2, ii : Nx-1, 1),...
            - R(1, ii : Nx-1, 2), R(1,ii : Nx-1, 1)]) ;
        
    b1(1)  =  2 *(R(1, ii, 1)   2 * alpha * S1) ;
    
    for jj = 2 : Nz - 1
        
        S  = sum(R(jj-1:jj 1, ii : Nx-1, :).*cat(3,[1;2;1],[1; -2; 1]),'all') ;
        b1(jj) =  2 *(R(jj, ii, 1)   alpha * S) ;
    end
end
toc