Huffman Coding using min priority queue-CodePudding

In this Question, I need to print the huffman code for all the data. But for the given test case below, I'm getting different output.

Input

i j k l m n o p

5 9 12 13 16 45 55 70

Where

First line enters the number of letters

Second line enters the letters

Third line enters the frequencies of the letters

Expected Output

n: 00

k: 0100

l: 0101

i: 01100

j: 01101

m: 0111

o: 10

p: 11

My Output

n: 00

o: 01

k: 1000

l: 1001

i: 10100

j: 10101

m: 1011

p: 11

My code

#include<bits/stdc  .h>
using namespace std;

struct Node {
    char data;
    int freq;
    Node *left, *right;
    Node(char x, int y): data(x), freq(y), left(NULL), right(NULL) {}
};

struct compare {
    bool operator()(Node *l, Node*r) {
        return l->freq > r->freq;
    }
};

void display(Node *p, string str) {
    if(p) {
        if(p->data != '$')
            cout << p->data << ": " << str << "\n";
        display(p->left, str   "0");
        display(p->right, str   "1");
    }
}

void huffmanCodes(char data[], int fr[], int n) {
    priority_queue<Node*, vector<Node*>, compare > pq;
    for(int i=0;i<n;i  )
        pq.push(new Node(data[i], fr[i]));
    while(pq.size() != 1) {
        Node *l = pq.top();
        pq.pop();
        Node *r = pq.top();
        pq.pop();
        Node *t = new Node('$', l->freq   r->freq);
        t->left = l;
        t->right = r; 
        pq.push(t);
    }
    display(pq.top(), "");
}

int main() {
    int n;
    cin >> n;
    char data[n];
    int freq[n];
    for(auto &x: data) cin >> x;
    for(auto &x: freq) cin >> x;
    huffmanCodes(data, freq, n);
}

CodePudding user response：

There isn't necessarily just one correct Huffman tree for a particular set of frequencies. If we look at yours, we initially have the following distribution

i:5 j:9 k:12 l:13 m:16 n:45 o:55 p:70

Combining the two smallest we get (ordered by frequency)

(ij):14 m:16 (kl):25 n:45 o:55 p:70

then again, combining the two smallest we get

(kl):25 (ij)(m):30 o:55 p:70

then after that, we get

n:45 (kl)((ij)(m)):55 o:55 p:70

Now here we have two entries with the same frequency (55), so we can combine n with either (kl)((ij)(m)) or o to form a new node - both will yield valid Huffman trees, both guaranteed to be optimal in terms of code size, so we can pick either one, and details of how the priority queue is implemented will determine which one actually gets picked in your case.

As long as the same strategy is used both for the encoder and decoder, this will work fine either way.

CodePudding user response：

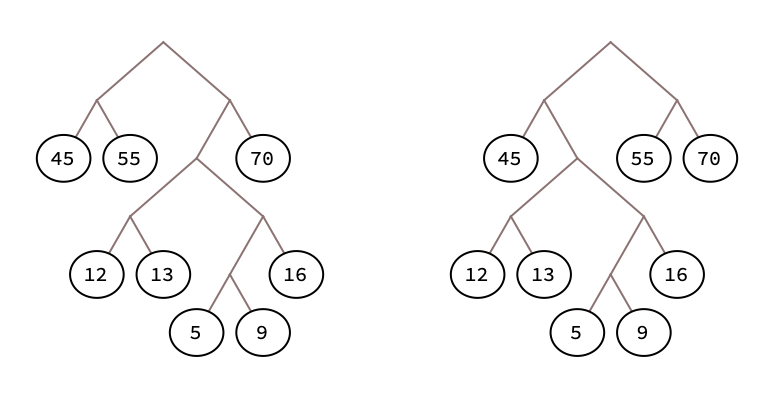
Just to add, depending on the choice made, you can get either of these trees, both of which are valid and optimal:

By the way, since you also show bit assignments, for each of those two trees, there are 32 ways to assign codes to the symbols, since you can make each branch individually 0 on the left and 1 on the right, or 1 on the left and 0 on the right. So there are actually 64 different ways to make valid Huffman codes for those frequencies.