How to plot interaction effects with individual-level variable and individual fixed-effects?-CodePudding

I have a dataset with individual id (factor), time t (factor), a dependent variable y (continuous) and an independent variable x (continuous), which can be measured at time t xt or can be set at the individual level xi.

set.seed(100)
df <- data.frame(id=as.factor(rep(1:20, each = 5)),
           t=as.factor(rep(1:5, 20)),
           y=rnorm(100, 5, 2))
df$xt <- rep(rnorm(100, 0, 1))
df$xi <- rep(rnorm(20, 0, 1), each = 5)

I want to estimate the marginal effects (and plot) of the interaction of time and the individual level IV (t:xi) while controlling for individual fixed effects (id). I know that the FEs of id absorb the effects of xi, but I want to see the effect of the interaction t:xi. Below I show how this works with t:xt but does not work with t:xi.

m1 <- lm(y ~ t   xt   t:xt   id, df)
m2 <- lm(y ~ t   xi   t:xi   id, df)

Effect(focal.predictors = c("t", "xt"), mod = m1)
Effect(focal.predictors = c("t", "xi"), mod = m2)

I have tried different combinations to write the interaction term (t t:xi, t*xi, etc.), and using different packages (effects, ggeffects, interplot, margins, etc.). Since there are coefficients for t and t:xi, I think there should be a way to estimate and plot these effects (using base-0/change). How could this be done?

CodePudding user response：

A less cumbersome way to estimate the same models that you posted in the answer to your own question would be to use the colon notation:

set.seed(100)
df <- data.frame(id=as.factor(rep(1:20, each = 5)),
           t=as.factor(rep(1:5, 20)),
           y=rnorm(100, 5, 2))
df$xt <- rep(rnorm(100, 0, 1))
df$xi <- rep(rnorm(20, 0, 1), each = 5)
df$t2_xi <- ifelse(df$t == 2, df$xi, 0)
df$t3_xi <- ifelse(df$t == 3, df$xi, 0)
df$t4_xi <- ifelse(df$t == 4, df$xi, 0)
df$t5_xi <- ifelse(df$t == 5, df$xi, 0)

m1 <- lm(y ~ t   t : xt   id, df)
m2 <- lm(y ~ t   t : xi   id, df)

You may also want to consider the marginaleffects package as an alternative for computing and plotting adjusted predictions and marginal effects. (Disclaimer: I am the author.)

library(marginaleffects)

plot_cap(m1, condition = c("xt", "t"))

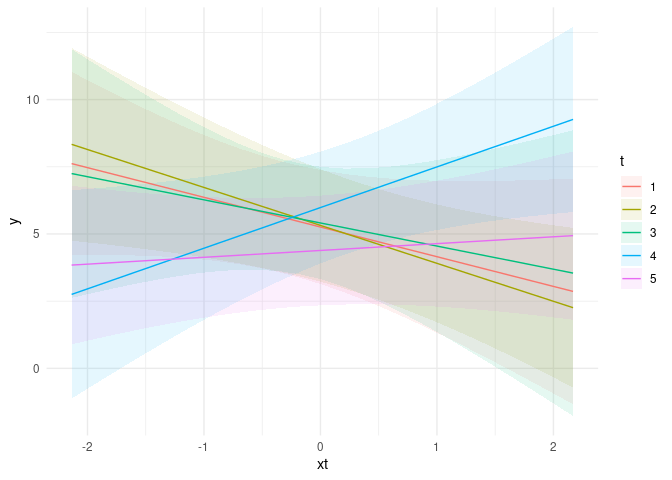
plot_cap(m2, condition = c("xi", "t"))

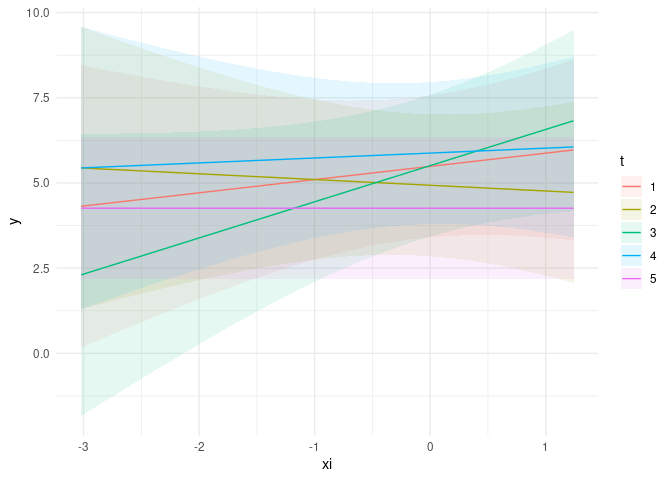
CodePudding user response：

Found a way to do it. It's a little clunky but it works. Basically, you have to create new variable for each interaction except for the first. It's not only that the individual FEs absorb the direct effect of xi, but they also absorb the interaction between xi and time t1. In other words, the baseline effect of xi in time 1 can be estimated based on the individual FEs.

df$t2_xi <- ifelse(df$t == 2, df$xi, 0)
df$t3_xi <- ifelse(df$t == 3, df$xi, 0)
df$t4_xi <- ifelse(df$t == 4, df$xi, 0)
df$t5_xi <- ifelse(df$t == 5, df$xi, 0)

m1 <- lm(y ~ t   t2_xi   t3_xi   t4_xi   t5_xi   id, df)

Effect(focal.predictors = c("t2_xi", "t3_xi", "t4_xi", "t5_xi"), mod = m1)