Why MATLAB figure is different than Scilab for the same model?-CodePudding

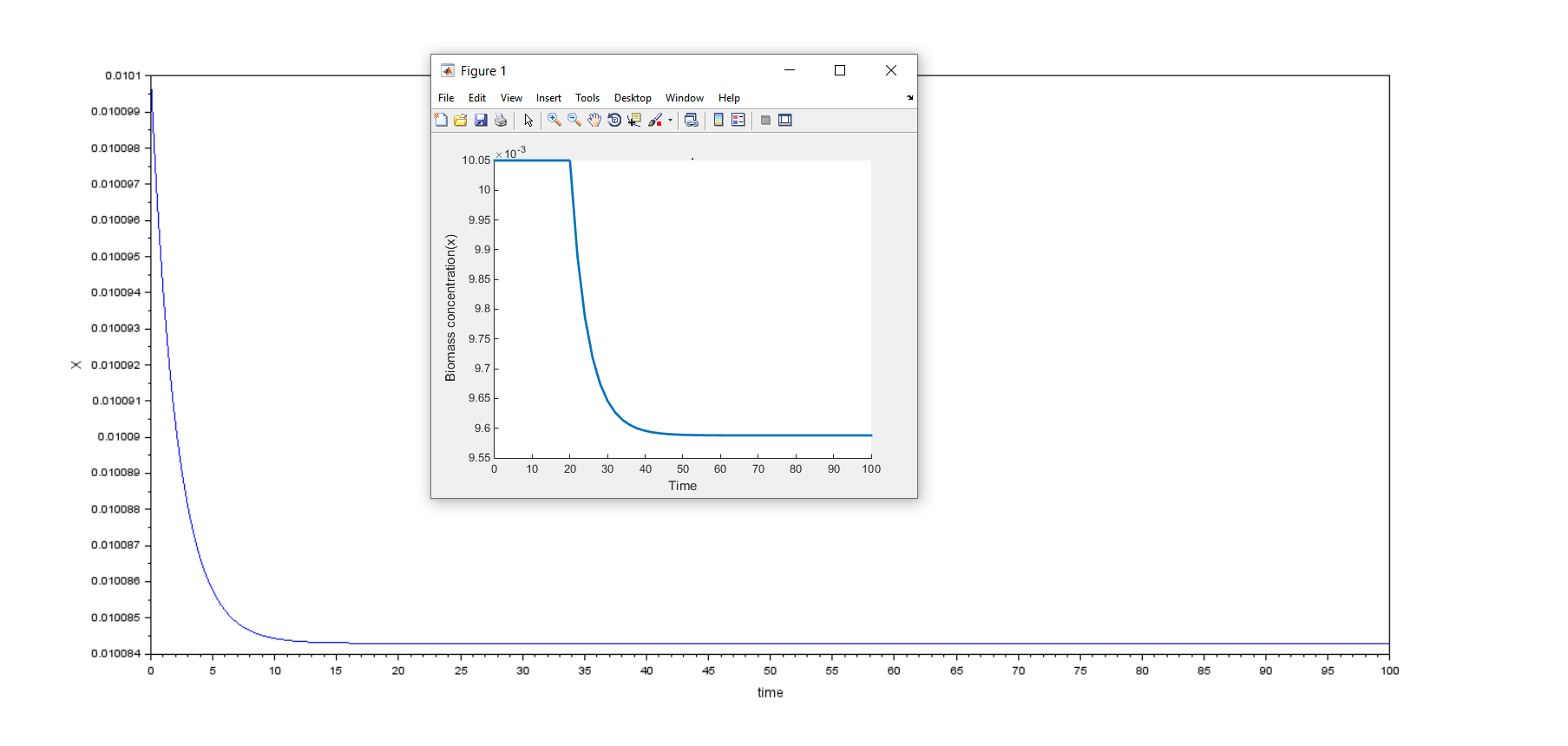
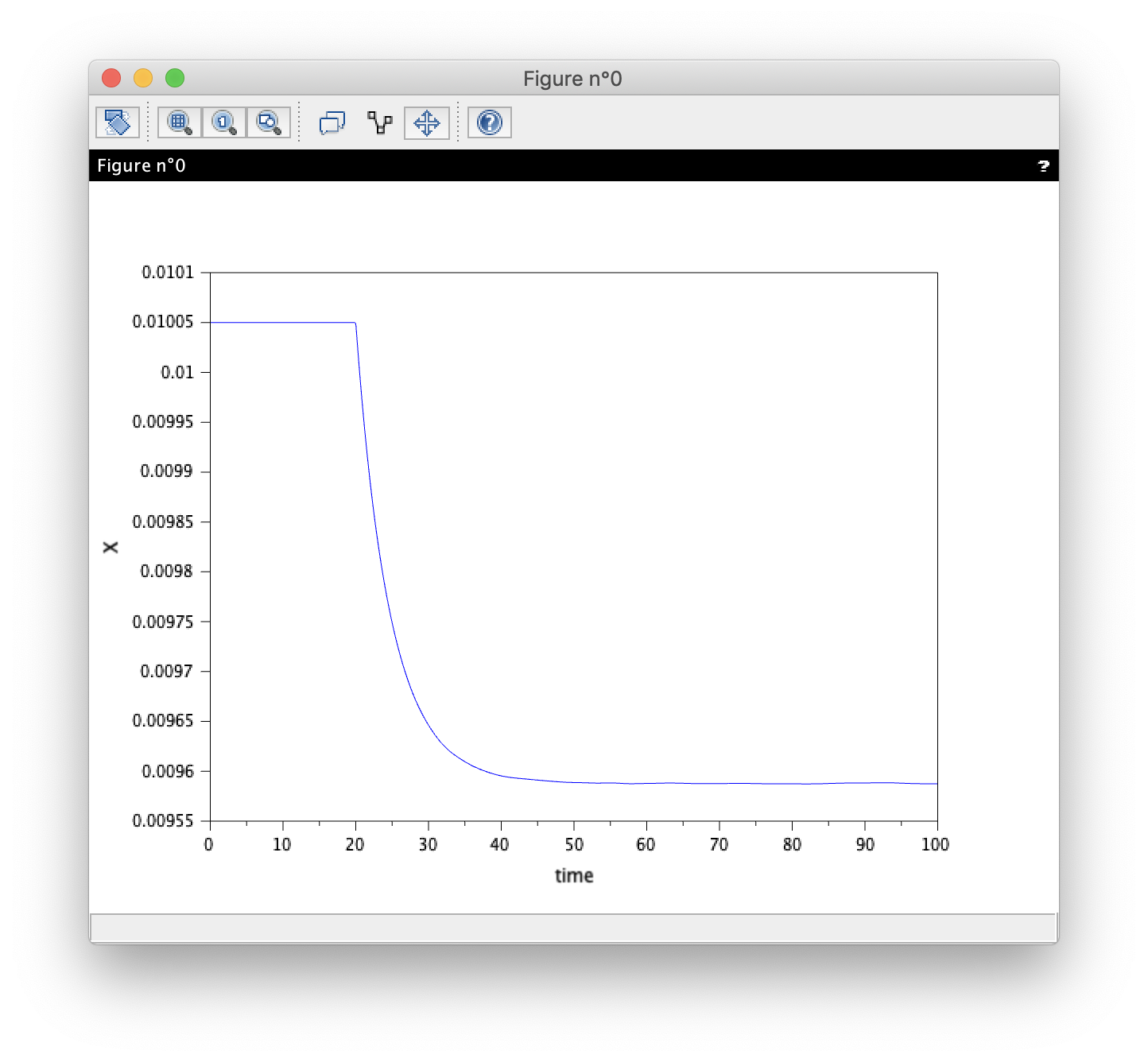
I am simulating a nonlinear system of ODEs by using an ode solver in Scilab, but when I simulated the same model with the same initial conditions in MATLAB Simulink I got a different figure than Scilab. I would like to understand what the wrong, I am going to attach my Scilab code and the two figures (MATLAB and Scilab outputs). here in my Scilab code, I am using Q as a unit step input of the given system. I would like to simulate the given system in Xcos, Can I get any help? because I tried to use a user-defined function block(Sci-function) like MATLAB to simulate this nonlinear system, but it does not work.

clc
clear
t = [0:100/999:100]
function U=step(t)

n= length(t);

U=zeros(n,1);   

for i=1:n

    if (t(i)>20)      //step time

        U(i) = 2.2;    //final value
    else
        U(i)=2   //initial value
        end
end

endfunction
//call a unit step function 
step    
Q=ans      //a unit step input
function dxdt=f(t,x)
    S=x(1);
    X=x(2);

    dxdt=[(Q/20)*(0.02-S)-((0.4/0.67)*(S*X)/(0.015 S))
    (-Q*X/20) (0.4*((S*X)/(0.015 S)))]
endfunction
t1=linspace(0,100,1000);
x0=[0.005;0.0101];
x=ode(x0,0,t1,f)
scf(0);clf(0)
plot(t1,x(2,:))
xlabel('time')
ylabel('X')

CodePudding user response：

The step should be computed within the right hand side of the ODE. If the rest of your ODE rhs is OK this should simulate what you want. Concerning your Matlab plot, the initial value was not the same as the one you used in your Scilab program (I fixed it):

clear
function dxdt=f(t,x)
    S=x(1);
    X=x(2);
    Q = 2; //initial value
    if (t>20)      //step time
        Q = 2.2;   //final value
    end
    dxdt = [(Q/20)*(0.02-S)-((0.4/0.67)*(S*X)/(0.015 S))
         (-Q*X/20) (0.4*((S*X)/(0.015 S)))]
endfunction

t1 = linspace(0,100,1000);
x0 = [0.005;0.01005];
x = ode(x0,0,t1,f)
scf(0);clf(0)
plot(t1,x(2,:))
xlabel('time')
ylabel('X')

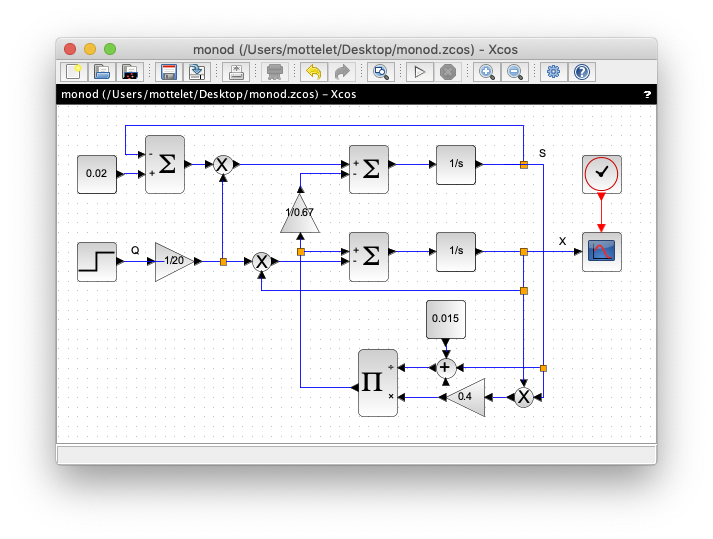
You can also simulate the system by using only native Xcos blocks :

You can get the diagram by using the following download link: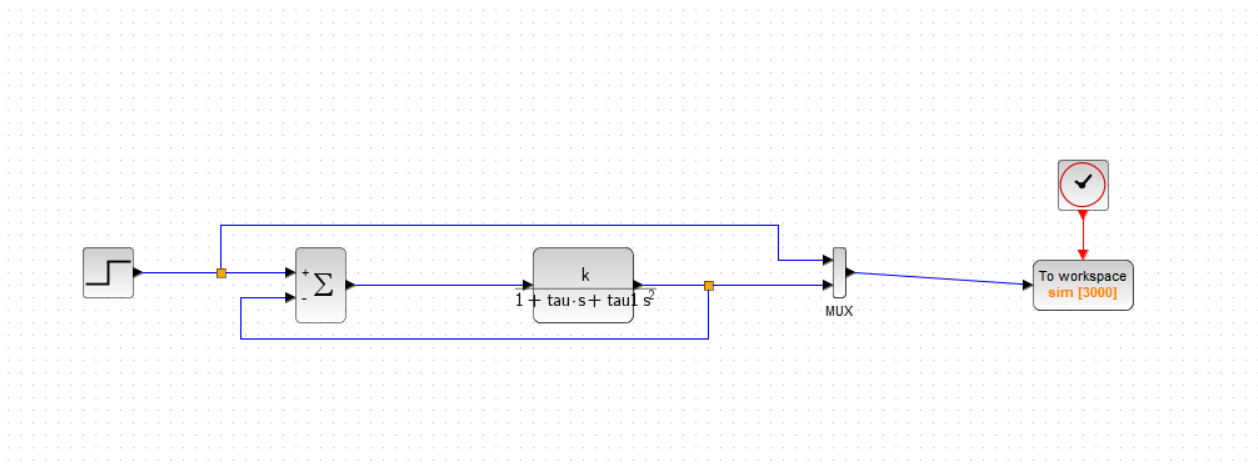

clear
//clear
clf
// load the blocks library and the simulation engine
context.k=100;
context.tau=1;
context.tau1=1;
loadXcosLibs(); 
loadScicos();

importXcosDiagram("cont.zcos")
typeof(scs_m)
//importXcosDiagram(pwd() "/Asserv_2nd_ordre.zcos");
        // Changement du contexte
        scs_m.props.context;
        // Simulation
        xcos_simulate(scs_m,4);
        // Change  values
scs_m.props.context = ["k=1000" "tau=10" "tau1=10"];
//for i=1:3
    //scs_m.props.context=scs_m.props.context(i)
//end
        xcos_simulate(scs_m, 4); //Xcos_compiler
sim

 t=sim.time
 in=sim.values(:,1)
out=sim.values(:,2)
scf(0);clf(0)
plot(t,in,t,out)
legend in out