Plot not starting from 0 while using numpy and matplotlib-CodePudding

So I am currently using numpy and matplotlib to do a math assignment, which is about the numerical differentiation method. So first I defined a mathematical function as follows:

def f_x(x):
y = -(3.71*x**2.3)
return y.real

Then I type in the code for the numerical differentiation:

def cal_derivative(a_function, x, delta_x, method): 
if method == "forward":
    delta_y = a_function(x   delta_x) - a_function(x)
    derivative = delta_y/(delta_x)
if method == "backward":
    delta_y = a_function(x).real - a_function(x - delta_x).real
    derivative = delta_y/(delta_x)
if method == "central":
    delta_y = a_function(x   delta_x).real - a_function(x - delta_x).real
    derivative = delta_y/(2*delta_x)
return derivative.real

Finally I plot the grpah of the numerical derivatives:

import numpy as np
import matplotlib.pyplot as plt
x_increment = 1
x_range = np.arange(0, 8 x_increment, x_increment)
y_1 = cal_derivative(f_x, x_range , 1, "forward")
y_2 = cal_derivative(f_x, x_range , 1, "backward")
y_3 = cal_derivative(f_x, x_range , 1, "central")
y_4 = analytical_derivative(x_range)
plt.plot(x_range,y_1,label = "Result for forward difference method")
plt.plot(x_range,y_2,label = "Result for backward backward method")
plt.plot(x_range,y_3,label = "Result for central divided difference method")
plt.plot(x_range,y_4,label = "Analytical differentiation result")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title("Result comparsion for x∈[0,8], Δx=1.0")
plt.ylabel("y")
plt.xlabel("x")

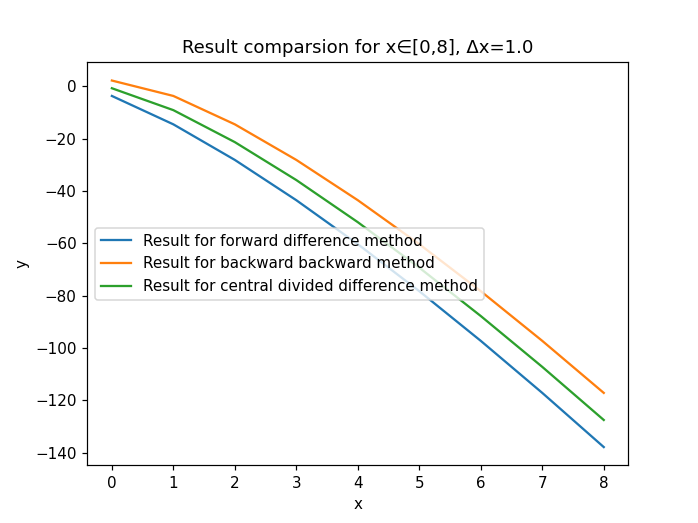
Then, I was expecting the output of my numerical differentiation code being plotted from x=0 to x=8 on a graph. However, I got something like this:

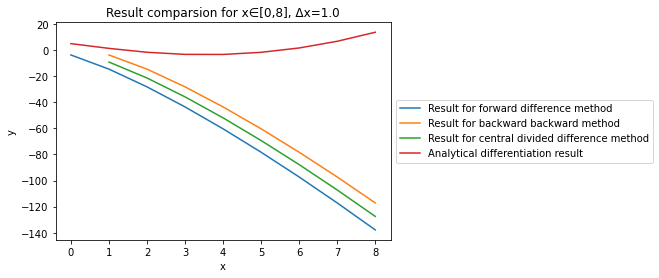
enter image description here

In the plot I got, the derivative for the backward and central difference method didn't start from 0 as I expected. I suspect that it is because for x<1 and delta_x = 1, my code involves a negative number raised to a fractional power (which is 2.3 for this case) and thus results in this bug, but I'm not sure. I tried many times to solve the issue but with no success. Could someone help me to solving this problem? Any help would be appreciated. Many thanks.

CodePudding user response：

You probably need to set x_range to be of complex type, like this:

x_range = np.arange(0, 8 x_increment, x_increment)   0j

In doing so, Numpy will be able to evaluate f_x computing complex values. If you were to use dtype=float in x_range (as you are doing right now), then the evaluation of f_x will create Nan values when x is negative.

Here I've removed the analytical solution since you didn't provide that function: