Using numpy where functions-CodePudding

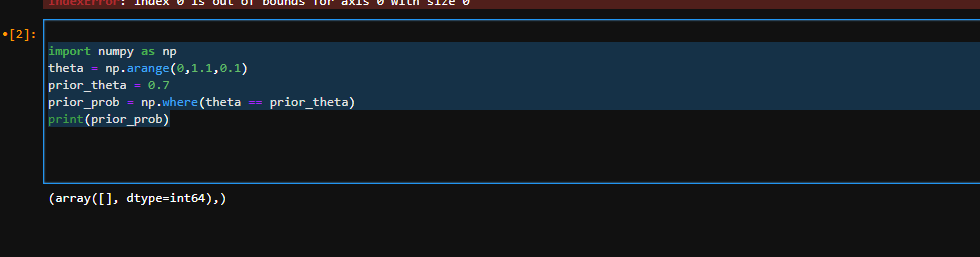
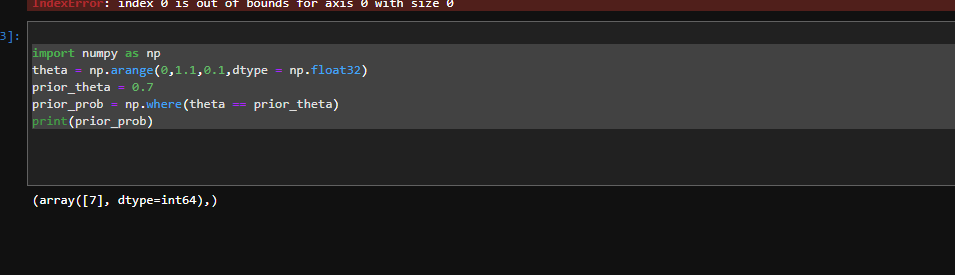
I am trying to understand the behavior of the following piece of code:

import numpy as np
theta = np.arange(0,1.1,0.1)
prior_theta = 0.7
prior_prob = np.where(theta == prior_theta)
print(prior_prob)

However if I explicitly give the datatype the where function works as per expectation

import numpy as np
theta = np.arange(0,1.1,0.1,dtype = np.float32)
prior_theta = 0.7
prior_prob = np.where(theta == prior_theta)
print(prior_prob)

This seems like a data type comparison. Any idea on this will be very helpful.

CodePudding user response：

This is just how floating point numbers work. You can't rely on exact comparisons. The number 0.7 cannot be represented in binary -- it is an infinitely repeating fraction. arange has to compute 0.1 0.1 0.1 0.1 etc,, and the round-off errors accumulate. The 7th value is not exactly the same as the literal value 0.7. The rounding is different for float32s, so you happened to get lucky.

You need to get in the habit of using "close enough" comparisons, like where(np.abs(theta-prior_theta) < 0.0001).

CodePudding user response：

np.isclose (and np.allclose) is useful when making floats tests.

In [240]: theta = np.arange(0,1.1,0.1)
In [241]: theta
Out[241]: array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])
In [242]: theta == 0.7
Out[242]: 
array([False, False, False, False, False, False, False, False, False,
       False, False])

np.arange warns us about using float increments - read the warnings section.

In [243]: theta.tolist()
Out[243]: 
[0.0,
 0.1,
 0.2,
 0.30000000000000004,
 0.4,
 0.5,
 0.6000000000000001,
 0.7000000000000001,
 0.8,
 0.9,
 1.0]
In [244]: np.isclose(theta, 0.7)
Out[244]: 
array([False, False, False, False, False, False, False,  True, False,
       False, False])
In [245]: np.nonzero(np.isclose(theta, 0.7))
Out[245]: (array([7]),)

arange suggests using np.linspace, but that's more to address the end point issue, which you've already handled with 1.1 value. The 0.7 value is still the same.