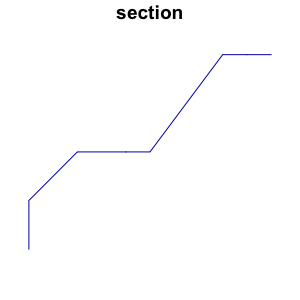
I'm trying to calculate the true length of each multilinestring that contains elevation data.

Here's my code:

library(sf)
#Linking to GEOS 3.10.2, GDAL 3.4.2, PROJ 9.0.0; sf_use_s2() is TRUE

# Data creation
s1 <- st_multilinestring(list(rbind(c(0,3,1), c(0,4,1))))
s2 <- st_multilinestring(list(rbind(c(0,4,1), c(1,5,4))))
s3 <- st_multilinestring(list(rbind(c(1,5,4), c(2,5,6))))
s4 <- st_multilinestring(list(rbind(c(2,5,6), c(2.5,5,12))))
s5 <- st_multilinestring(list(rbind(c(2.5,5,12), c(4,7,4))))
s6 <- st_multilinestring(list(rbind(c(4,7,4), c(4.5,7,3))))
s7 <- st_multilinestring(list(rbind(c(4.5,7,3), c(5,7,3))))

sf_ml <- st_sf(section = 1,
               geometry=st_sfc(list(s1,s2,s3,s4,s5,s6,s7)),
               crs = 4326)
plot(sf_ml)

However, when using the st_length() it prompts that it is dropping the Z coordinate. Thus, I'm thinking that it is not using the elevation values.

st_length(sf_ml)
# st_as_s2(): dropping Z and/or M coordinate
#Units: [m]
#[1] 111195.10 157010.41 110771.96  55385.98 277435.26  55183.13  55183.13

And if I don't use S2, I'm getting a different set of values.

sf_use_s2(F)
#Spherical geometry (s2) switched off

st_length(sf_ml)
#Units: [m]
#[1] 110578.44 156665.64 110898.70  55449.35 276575.59  55247.61  55247.61

If I don't use S2, does st_length() make use of the elevation values? Or am I using the wrong R package for this?

Thanks in advance.

CodePudding user response：

The st_length calculation does use the Z values when working with lat-long data.

Let's create a single feature that is 1m along and 1m up. I'll do this in a UK projected system and convert to lat-long in a bit.

> g1 = st_multilinestring(list(rbind(c(0,1,2),c(0,2,3))))
> sd = st_sf(geometry=st_sfc(g1), crs=27700)

st_length ignores the Z, silently, and gives a 1m length:

> st_length(sd)
1 [m]

This is independent of s2 status, of course, because we are in a cartesian coordinate system:

> sf_use_s2(TRUE)
> st_length(sd)
1 [m]
> sf_use_s2(FALSE)
Spherical geometry (s2) switched off
> st_length(sd)
1 [m]

Now transform to 4326 and see:

> sdg = st_transform(sd, 4326)
> sf_use_s2(TRUE)
Spherical geometry (s2) switched on
> st_length(sdg)
st_as_s2(): dropping Z and/or M coordinate
0.9981138 [m]

This has dropped the Z and returned a distance a bit less than 1m because of the transformation. Now without s2:

> sf_use_s2(FALSE)
Spherical geometry (s2) switched off
> st_length(sdg)
1.413078 [m]

This is approximately sqrt(2), which is the 3d distance including the Z of this line - but there must have been some conversion back to meters to return a distance of meters (and treat the Z coord as being in meters). This is mentioned in the details of ?st_length and will be using a spherical distance - maybe it computes that for the X-Y distance and then combines with the Z distance via Pythagoras theorem.

So I conclude by observation:

• For projected cartesian coordinates, st_length silently ignores Z
• For lat-long coordinates with s2 enabled, st_length noisily drops Z
• For lat-long coordinates with s2 disables, st_length computes 3d distance using Z