Intro
For the N-body simulation I need to calculate the total received force Fi for each body it receives from the other bodies. This is an O(n^2) problem, because for each body the pairwise total force must be calculated. Because of the Newton's 3rd axiom fi,j = -fi,j we can reduce the number of force calculations by half.
Problem
How to implement this law in my code in order to optimize the acceleration calculation?
What I have did so far?
I programmed the total received force for each body, but without that optimization.
std::vector<glm::vec3> SequentialAccelerationCalculationImpl::calcAccelerations(
const std::vector<Body> &bodies,
const float softening_factor
) {
const float softening_factor_squared = softening_factor * softening_factor;
const size_t num_bodies = bodies.size();
std::vector<glm::vec3> accelerations(num_bodies);
// O(n^2)
for (size_t i = 0; i < num_bodies; i) {
glm::vec3 received_total_force(0.0);
for (size_t j = 0; j < num_bodies; j) { // TODO this can be reduced to half
if (i != j) {
const glm::vec3 distance_vector = bodies[i].getCurrentPosition() - bodies[j].getCurrentPosition();
float distance_squared =
(distance_vector.x * distance_vector.x)
(distance_vector.y * distance_vector.y)
(distance_vector.z * distance_vector.z);
// to avoid zero in the following division
distance_squared = softening_factor_squared;
received_total_force = ((bodies[j].getMass() / distance_squared) * glm::normalize(distance_vector));
}
}
accelerations[i] = GRAVITATIONAL_CONSTANT * received_total_force;
}
return accelerations;
}
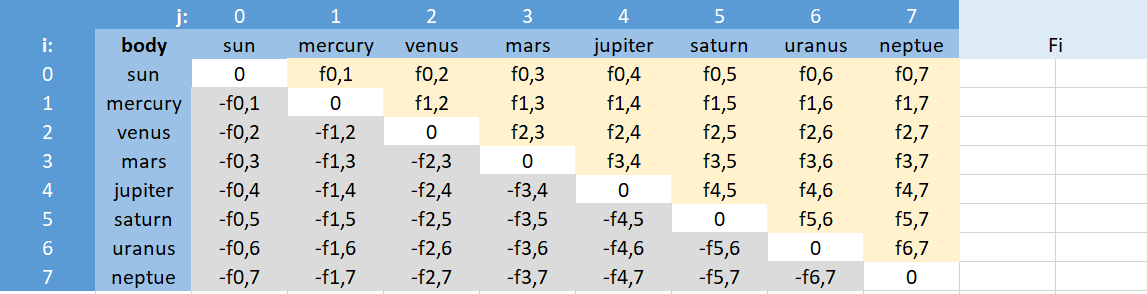
I also sketched the force matrix:
CodePudding user response:
The simple solution is to have the inner loop start from i 1 instead of from 0:
for (size_t i = 0; i < num_bodies; i) {
glm::vec3 received_total_force(0.0);
for (size_t j = i 1; j < num_bodies; j) {
glm::vec3 distance_squared = glm::distance2(bodies[i].getCurrentPosition(), bodies[j].getCurrentPosition());
...
}
}
However now you have to ensure you update both accelerations[i] and accelerations[j] inside the inner loop, instead of first accumulating in received_total_force:
accelerations[i] = bodies[j].getMass() / distance_squared * glm::normalize(distance_vector);
accelerations[j] -= bodies[i].getMass() / distance_squared * glm::normalize(distance_vector);
