Solving a linear model for a known value of y in R-CodePudding

I have a series of x and y values that I've used to build a linear model. I can use predict() to find a value of y from a known value of x, but I'm struggling to calculate x from a known value of y. I've seen a few posts that talk about using the approx() function, but I can't figure out how to implement it for my use case. The idea is to write a function that takes a numerical value of y as an input and returns the expected value of x that it would correspond to, ideally with a prediction interval, eg "The expected value of x is 38.90, plus or minus 0.7", or something like that.

Here's my data:

> dput(x)
c(4.66, 5.53, 5.62, 5.85, 6.26, 6.91, 7.04, 7.32, 7.43, 7.85, 
8.1, 8.3, 8.34, 8.53, 8.69, 8.7, 8.73, 8.76, 8.96, 9.06, 9.42, 
9.78, 10.3, 10.82, 10.98, 11.07, 11.09, 11.32, 11.75, 12.1, 12.46, 
12.5, 12.99, 13.02, 13.28, 13.43, 13.96, 14, 14.07, 14.29, 14.57, 
14.66, 15.21, 15.56, 15.97, 16.44, 16.8, 17.95, 18.33, 18.62, 
18.92, 19.49, 19.9, 19.92, 20.14, 20.18, 21.19, 22.7, 23.25, 
23.48, 23.49, 23.58, 23.7, 23.83, 23.83, 23.97, 24.05, 24.14, 
24.15, 24.19, 24.32, 24.62, 24.9, 24.92, 25, 25.06, 25.31, 25.36, 
25.86, 25.9, 25.95, 25.99, 26.08, 26.2, 26.27, 26.39, 26.5, 26.51, 
26.68, 26.78, 26.82, 26.92, 26.92, 27.05, 27.05, 27.07, 27.32, 
27.6, 27.77, 27.8, 27.91, 27.96, 27.97, 28.04, 28.05, 28.15, 
28.2, 28.28, 28.37, 28.51, 28.53, 28.53, 28.66, 28.68, 28.72, 
28.74, 28.82, 28.83, 28.83, 28.86, 28.89, 28.91, 29.04, 29.2, 
29.35, 29.4, 29.42, 29.48, 29.53, 29.65, 29.67, 29.69, 29.7, 
29.72, 29.93, 29.97, 30.03, 30.08, 30.09, 30.11, 30.18, 30.62, 
30.66, 30.78, 31, 31.32, 31.43, 31.47, 31.69, 31.96, 32.33, 32.5, 
32.5, 32.58, 32.7, 32.92, 33.2, 33.6, 33.72, 33.77, 33.95, 34.02, 
34.08, 34.42, 34.79, 34.91, 34.99, 35.08, 35.15, 35.49, 35.6, 
35.6, 35.74, 35.8, 36.05, 36.17, 36.3, 36.37, 36.84, 37.31, 37.95, 
38.75, 38.78, 38.81, 38.9, 39.21, 39.31, 39.5, 42.68, 43.92, 
43.95, 44.64, 45.7, 45.95, 46.25, 46.8, 49.08, 50.33, 51.23, 
52.76, 53.06, 62)
> dput(y)
c(11.91, 13.491, 13.708, 13.984, 14.624, 15.688, 15.823, 16.105, 
16.387, 17.004, 17.239, 17.498, 17.686, 17.844, 17.997, 18.044, 
18.003, 18.191, 18.332, 18.25, 18.778, 19.237, 19.693, 20.177, 
20.441, 20.876, 20.512, 20.894, 21.493, 21.539, 21.951, 21.763, 
22.498, 22.451, 22.744, 22.785, 23.409, 23.314, 23.408, 23.567, 
23.849, 23.978, 24.472, 24.678, 25.236, 25.547, 25.676, 26.81, 
26.83, 27.275, 27.331, 27.844, 28.009, 28.244, 28.497, 28.555, 
29.067, 30.412, 30.788, 30.965, 31.058, 31.423, 31.346, 31.118, 
31.252, 31.258, 31.399, 31.605, 31.552, 31.881, 31.822, 31.91, 
32.333, 32.174, 32.222, 32.704, 32.445, 32.557, 32.993, 32.845, 
32.997, 32.909, 32.911, 33.121, 33.191, 33.156, 33.426, 33.332, 
33.52, 33.526, 33.697, 33.379, 33.849, 33.726, 33.538, 33.885, 
33.961, 34.284, 34.208, 33.896, 34.278, 34.355, 34.276, 34.267, 
34.399, 34.507, 34.492, 34.531, 34.695, 34.642, 34.872, 34.772, 
34.813, 34.942, 34.883, 34.948, 34.719, 34.983, 34.99, 35.136, 
35.007, 34.026, 35.148, 35.201, 35.459, 35.418, 35.236, 35.411, 
35.459, 35.5, 35.665, 35.724, 35.636, 35.667, 35.747, 35.788, 
35.882, 35.9, 35.83, 36.106, 36.029, 36.364, 36.358, 36.517, 
37.005, 36.74, 36.963, 36.634, 37.04, 37.48, 37.581, 37.78, 37.686, 
38.262, 37.998, 37.986, 38.498, 39.296, 38.467, 38.779, 38.885, 
38.72, 39.038, 38.932, 39.719, 39.654, 39.367, 40.072, 39.707, 
39.742, 39.919, 40.054, 40.189, 40.197, 40.154, 40.383, 42.146, 
40.595, 40.971, 41.441, 41.964, 42.328, 42.463, 42.627, 42.633, 
42.721, 42.786, 42.857, 45.318, 45.665, 46.406, 46.335, 47.663, 
47.181, 48.074, 48.109, 49.931, 50.377, 51.053, 52.451, 53.004, 
65.889)
> model <- lm(y ~ poly(x,3,raw=TRUE))
> model

Call:
lm(formula = y ~ poly(x, 3, raw = TRUE))

Coefficients:
            (Intercept)  poly(x, 3, raw = TRUE)1  poly(x, 3, raw = TRUE)2  poly(x, 3, raw = TRUE)3  
              6.6096981                1.4736619               -0.0238935                0.0002445

CodePudding user response：

Since you have fitted a low order polynomial in ordinary form (raw = TRUE), you can use polyroot to directly find x given y.

## pc: polynomial coefficients in increasing order
solvePC <- function (pc, y) {
  pc[1] <- pc[1] - y
  ## all roots, including complex ones
  roots <- polyroot(pc)
  ## keep real roots
  Re(roots)[abs(Im(roots)) / Mod(roots) < 1e-10]
}

y0 <- 38.9  ## example y-value
x0 <- solvePC(coef(model), y0)
#[1] 34.28348

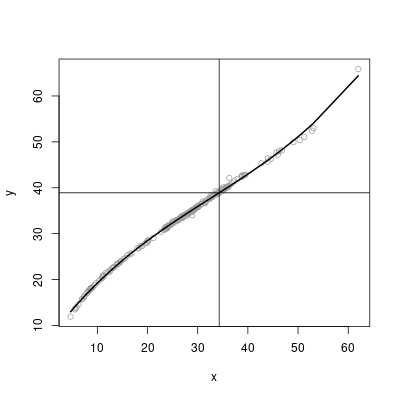
plot(x, y, col = 8)
lines(x, model$fitted, lwd = 2)
abline(h = y0)
abline(v = x0)

To get an interval estimate, we can use sampling methods.

## polyfit: an ordinary polynomial regression model fitted by lm()
rootCI <- function (polyfit, y, nSamples = 1000, level = 0.05) {
  ## sample regression coefficients from their joint distribution
  pc <- MASS::mvrnorm(nSamples, coef(polyfit), vcov(polyfit))
  ## for each row (a sample), call solvePC()
  roots <- apply(pc, 1, solvePC, y)
  ## confidence interval
  quantile(roots, prob = c(0.5 * level, 1 - 0.5 * level))
}

## 95% confidence interval
rootCI(model, y = y0)
#    2.5%    97.5% 
#34.17981 34.38828

CodePudding user response：

You can use optim:

Predict the y values given x:

pred_y <- function(x)predict(model, data.frame(x))
pred_y(x = 10)
[1] 19.20145

Now to predict x given y, we do:

pred_x <- function(y) optim(1, \(x) (y-pred_y(x))^2, method='BFGS')[[1]]
pred_x(19.20145)
[1] 10

CodePudding user response：

The uniroot function is intended for this type of problem.

#coefficients for the model
coeff <- c(6.6096981, 1.4736619, -0.0238935, 0.0002445)


#define the equation which one needs the root of
modely <- function(x, y) { 
 # could use the predict function here
   my<-coeff[1]   coeff[2]*x   coeff[3]*x**2   coeff[4]*x**3
   y-my
}

#use the uniroot functiion
#In this example y=10
uniroot(modely, lower=-100, upper=100, y=10)

$root
[1] 2.391022

$f.root
[1] -1.208443e-08

$iter
[1] 10

$init.it
[1] NA

$estim.prec
[1] 6.103516e-05

In this case for y=10, x = 2.391022