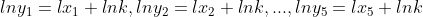How to find variables in Julia using Linear Regression for Interpolation method?-CodePudding

There is an unknown function 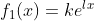, and there are unknown coefficients k, l. Task is to estimate k, l using linear regression, through the data table.

-2.0  1.719334581463762
-1.0  1.900158577875515
0.0   2.1
1.0   2.3208589279588603
2.0   2.5649457921363568

Till now mathematically I did like, taking logarithm on both sides

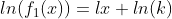
Then using the data table, 5 equations will be formed

Now apply the linear regressor, to this logarithm-transformed data, to estimate the coefficients k and l.

I have built a linear regresor,

using DataFrames, GLM

function LinearRegression(X)
    x = X[:,1]
    y = X[:,2]
    data = DataFrame(y = y, x = x)
    reg = lm(@formula(y ~ x), data)
    return coef(reg)[2], coef(reg)[1]
end

Any solution to how to find l and k values using this technique?

CodePudding user response：

You're almost there, but I think you have a misconception mathematically in your code. You are right that taking the log of f(x) makes this essentially a linear fit (of form y = mx b) but you haven't told the code that, i.e. your LinearRegression function should read:

function LinearRegression(X)
    x = X[:,1]
    y = X[:,2]
    data = DataFrame(y = log.(y), x = x)
    reg = lm(@formula(y ~ x), data)
    return coef(reg)[2], coef(reg)[1]
end

Note that I have written y = log.(y) to match the formula as otherwise you are fitting a line to exponential data. We don't take the log of x because it has negative values. Your function will then return the correct coefficients l and log(k) (so if you want just k itself you need to take the exponential) -- see this plot as proof that it fits the data perfectly!

CodePudding user response：

You need to convert the intercept with exp and the slope keeps as it is.

using Statistics #mean

#Data
X = [-2.0  1.719334581463762
     -1.0  1.900158577875515
     0.0   2.1
     1.0   2.3208589279588603
     2.0   2.5649457921363568]

x = X[:,1]
y = X[:,2]
yl = log.(y)

#Get a and b for: log.(y) = a   b*x
b = x \ yl
a = mean(yl) - b * mean(x)

l = b
#0.10000000000000005
k = exp(a)
#2.1

k*exp.(l.*x)
#5-element Vector{Float64}:
# 1.719334581463762
# 1.900158577875515
# 2.1
# 2.3208589279588603
# 2.5649457921363568