`std::stable_sort` gives wrong results when `std::execution::par`-CodePudding

I wrote simple algorithm for sorting rows in Eigen matrix. This should do the same as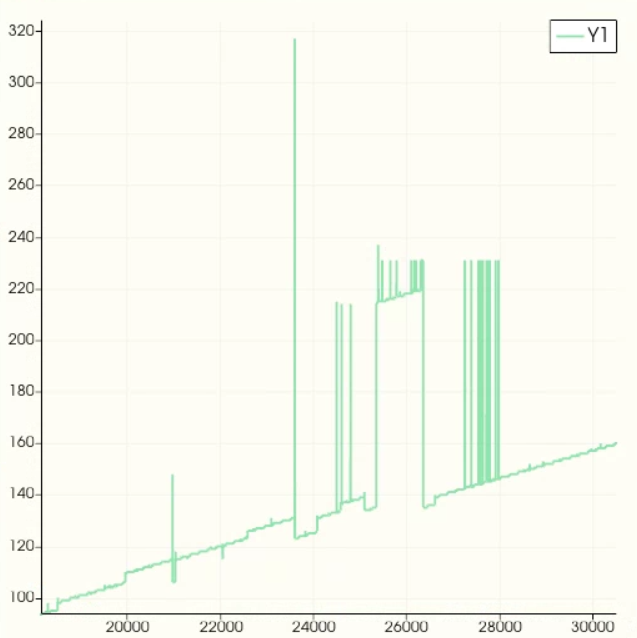

With std::execution::seq and the same data the graph non-decreasingly grows in steps (correct result).

What should I know about execution policy to avoid such situations?

EDIT: my implementation for sort_rows that now works with std::execution::par and doesn't use recursion anymore:

template <typename D>
void _sort(
    const D &M,
    Eigen::VectorX<ptrdiff_t>& idx,
    std::function<bool(ptrdiff_t, ptrdiff_t)> cmp_fun)
{
  // initialize original index locations
  idx = Eigen::ArrayX<ptrdiff_t>::LinSpaced(
        M.rows(), 0, M.rows()-1);

  std::stable_sort(std::execution::par, idx.begin(), idx.end(), cmp_fun);
}


/// \brief sort_rows  sorts the rows of a matrix in ascending order
/// based on the elements in the first column. When the first column
/// contains repeated elements, sortrows sorts according to the values
/// in the next column and repeats this behavior for succeeding equal values.
/// M_sorted = M(ind, Eigen::all)
/// \param M
/// \return ind
template <typename D>
Eigen::VectorX<ptrdiff_t> sort_rows(const Eigen::DenseBase<D> &M){

  // initialize original index locations
  Eigen::VectorX<ptrdiff_t> idx;

  std::function<bool(ptrdiff_t, ptrdiff_t)> cmp_fun;
  cmp_fun = [&M](
      const ptrdiff_t& row1,
      const ptrdiff_t& row2)->bool
  {
    ptrdiff_t N = M.cols()-1;
    for (ptrdiff_t col = 0; col < N; col  ){
      if (M(row1, col) < M(row2, col))
        return true;

      if (M(row1, col) > M(row2, col))
        return false;
    }

    // notice the operator is '<=' as it is the last column check
    // i.e. when all other columns are equal at these rows
    if (M(row1, Eigen::last) <= M(row2, Eigen::last))
      return true;

    return false;
  };

  _sort(M.derived(), idx, cmp_fun);

  return idx;
}

CodePudding user response：

Here is my implementation of rowsort. I find the documentation of rowsort somewhat confusing. I work under the assumption that it is just a lexicographical sort.

Note that your code can probably be fixed just by making a col variable local to your lambda instead of having it as a shared reference.

template<class Derived>
void rowsort(Eigen::MatrixBase<Derived>& mat)
{
    using PermutationMatrix = 
          Eigen::PermutationMatrix<Derived::RowsAtCompileTime>;
    PermutationMatrix permut;
    permut.setIdentity(mat.rows());
    auto& indices = permut.indices();
    std::stable_sort(std::execution::par, indices.begin(), indices.end(),
          [&mat](Eigen::Index left, Eigen::Index right) noexcept -> bool          
          {
              const auto& leftrow = mat.row(left);
              const auto& rightrow = mat.row(right);
              for(Eigen::Index col = 0, cols = mat.cols();
                    col < cols;   col) {
                  const auto& leftval = leftrow[col];
                  const auto& rightval = rightrow[col];
                  if(leftval < rightval)
                      return true;
                  if(leftval > rightval)
                      break;
              }
              return false;
          });
    mat = permut.inverse() * mat;
}

Notes:

There might be a clever way to avoid inverting the permutation.
It's a bit annoying that applying the permutation is only defined for MatrixBase, not DenseBase
stable sort isn't necessary for this. I assume you have an external reason for using it
The function should probably take the matrix as a const reference so that it can be called seamlessly with block() expressions and then cast away the const. I didn't put it in to avoid making the code ugly and confusing. Refer to the relevant chapter in the documentation on passing Eigen types to functions

CodePudding user response：

You can do this almost out-of-the-box using Eigen's iterator interface and std::lexicographical_compare:

std::sort(A.rowwise().begin(), A.rowwise().end(),
  [](auto const& r1, auto const& r2){
     return std::lexicographical_compare(r1.begin(), r1.end(), r2.begin(), r2.end());});

Unfortunately, you first need to declare an Eigen::swap function for this to work (this may get fixed in later versions -- see also this related question: https://stackoverflow.com/a/71556445/):

namespace Eigen {
    template<class T>
    void swap(T&& a, T&& b){
        a.swap(b);
    }
}

And see this for a working example: https://godbolt.org/z/7P1hYTn65

Your initial plan of sorting an index-list and doing just one permutation could actually be faster for large rows (I did not benchmark this).