I'd like to draw an arc segment:

(90° here, but I want different arcs, for something like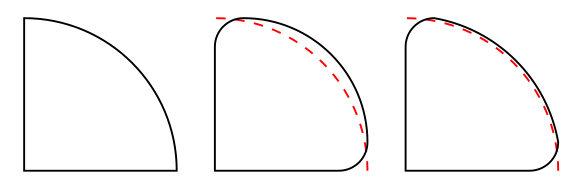

The first has the path definition (center of the arc at 0, 100).

d="M 0,100 H 80 A 80,80 0 0 0 0,20 z"

In the second one, the corners have been rounded with a radius of 15. To keep the connection of the small corner arcs with the larger arc smooth, the larger radius is reduced from 80 to 65. As you can see, the arc sits wide outside its original position.

d="M 0,100 H 65 A 15,15 0 0 0 80,85 65,65 0 0 0 15,20 15,15 0 0 0 0,35 Z"

In the third one, the connection is ignored and the radius kept at 80. Still, the position of the arc is too wide.

d="M 0,100 H 65 A 15,15 0 0 0 80,85 80,80 0 0 0 15,20 15,15 0 0 0 0,35 Z"

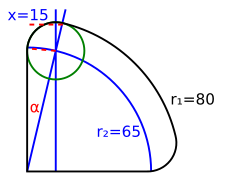
That is because the small corner arc is too far from the center of the large arc. For a visual construction, you would draw a circle with radius 15 inside the pie, and move it towards the corner until it meets both the straight line and the arc in a tangent. See the green circle:

It is meeting the arc to the right of the upper corner, and a bit lower. How much lower, you have to compute.

Suppose you want to round the corner with a radius of d=15. Then, the center of the circle sits at the intersection of the vertical line at x = d = 15 and the reduced arc with r₂ = r₁ - d = 65.

The angle α of a line from the inner corner to that point computes to

α = arcsin(d / r₂) = arcsin(15 / 65) = 13.342364°

The end point of the large arc then is at

x = cx   r₁ × sin(α) = 80 × sin(13.342364°) = 18.4615
y = cy - r₁ × cos(α) = 100 - 80 × cos(13.342364°) = 22.1593

The point where the rounded corner begins is at

x = cx = 0
y = cy - r₂ × cos(α) = 100 - 65 × cos(13.342364°) = 36.7544

After doing the same computation for the lower right corner, the final path computes to

d="M 0,100 H 63.25 A 15,15 0 0 0 77.85,81.54 80,80 0 0 0 18.46,22.15 15,15 0 0 0 0,36.75 Z"