For the following question:

Consider a directed graph with distinct and nonnegative edge lengths and a source vertex s. Fix a destination vertex t, and assume that the graph contains at least one s-t path. Which of the following statements are true?

• The shortest s-t path must exclude the maximum-length edge of G.
• There is a shortest s-t path with no repeated vertices (i.e., a "simple" or "loopless" such path).
• The shortest (i.e., minimum-length) s-t path might have as many as n – 1 edges, where n is the number of vertices.
• The shortest s-t path must include the minimum-length edge of G.

I had checked the last option, but got this feedback:

The statement "The shortest s-t path must include the minimum-length edge of G." is incorrect.

Could anyone help me to picture a counterexample of this? Is it because if there is a loop, the length edge of G won't be the length from its source to its destination?

CodePudding user response：

The edges that are on the shortest path between s and t do not need to include the shortest nor the longest edge of the graph. A trivial example is where s and t are the ends of the same edge, and that is the only path between s and t: that means there really isn't a choice... it is that edge, and no other edge, irrespective of the lengths of any of the edges in the graph.

It has nothing to do with loops.

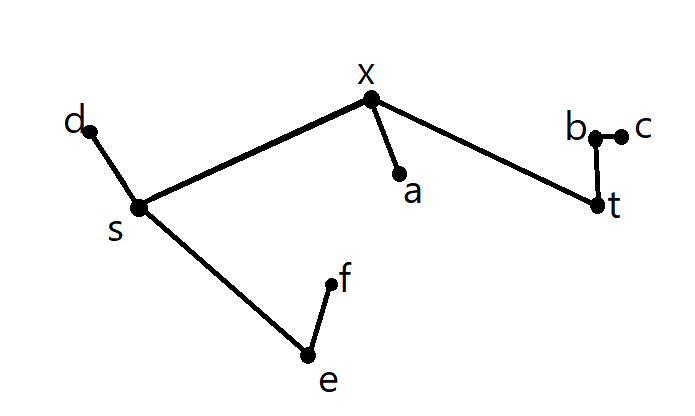
Here is another example:

Also here there is one path between s and t, and it is clear there are many edges in the graph that have a lesser length than the two edges that are on the path between s and t.