Is this problem solvable in polynomial time?-CodePudding

Upd: Now I have a O(n^3) algo.

I'm trying to come up with a reasonable algorithm for this problem:

There are some pairs:

(1,2),(1,3),...,(1,n),  
(2,3),(2,4),...,(2,n),  
...  
(n-2,n-1),(n-2,n),  
(n-1,n)

And there are m conditions(m >= n), each like that at most one of [pair a, pair b, pair c, ...] can be selected. Each condition includes some pairs(maybe 1,2,3,...). And each pair is included in exactly one condition.

Now can we find a plan to select n pairs, satisfy that all numbers from 1 to n are included in exactly 2 pairs?

Only need to judge if it is possible.

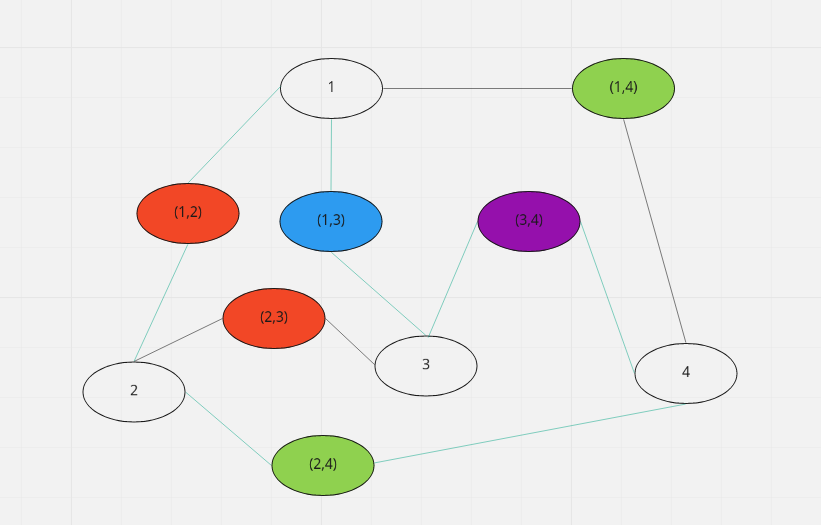
For example, when n = 4 and the conditions are [{(1,2),(2,3)},{(1,3)},{(1,4),(2,4)},{(3,4)}], select (1,2),(1,3),(2,4),(3,4) is ok.

If it is NP-hard, can we find an algorithm which time complexity is lower than 2^(n^2/4)?

Unfortunately now I only have an algo that enumerate all possible situations. It's worst time complexity is 2^(n^2/4).

Nocite that time complexity like n^m is not polynomial.

CodePudding user response：

Solution not found yet. But there is a combinatorial point of view which is worth mentioning.

Consider your pairs are vertices of a graph. Also, add n vertices labeled 1, ... , n.

Add undirected edges between a vertex i (i in [1..n]) and all vertices corresponding to pairs that contain i.

For each condition, paint all vertices in the condition with a different color. In the end, you will have painted all vertices of the graph (except the vertices labeled 1, ..., n) and each vertex will have exactly one color.

Your problem can be translated into selecting at most one vertex of each color such that the graph induced by the selected vertices and the vertices 1,...,n is such that each of the vertices 1,...,n has degree exactly 2.

A solution for your example is illustrated in the image below (the induced graph is with blue edges):

Notice that a solution for the general version of the problem is always a simple cycle of length 2*n of the form p(1)--v(1)--p(2)--v(2)--...--p(n)--v(n)--p(1) such that the colors of v(1), ..., v(n) are all different and p(1), ..., p(n) is a permutation of 1,..., n.