how to multiply 2bit * 2bit using 1 bit full-adder?-CodePudding

First, an example of what the task is about:

For example we have the two 2-bit binary numbers: y1y0 and x1x0, so y1 is one bit big, y0 too, the same for x1 and x0, together these are two 2-bit numbers.

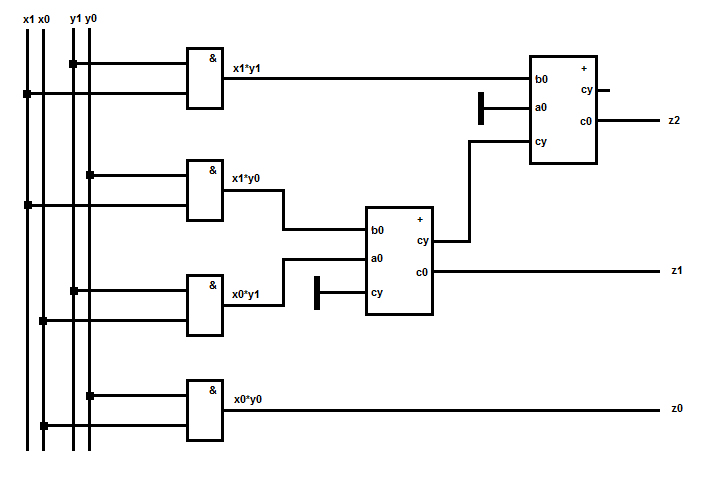
Now we have to calculate the product: z=y1y0*x1x0, only with and gates and a 3 bit full adder this is trivial (Solution for this Task with 3 bit adder):

Solution for this Task with 3 bit adder

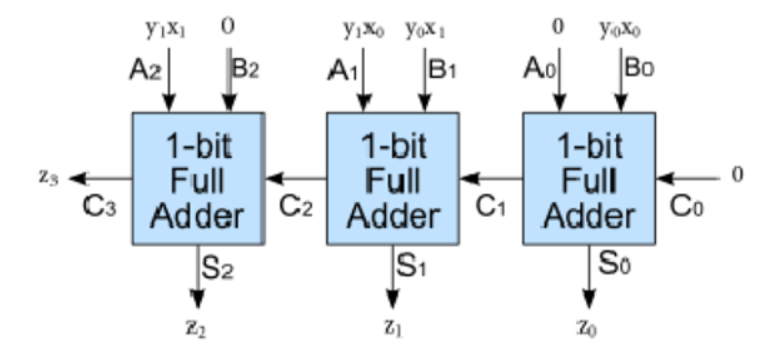
Here one must note, however, that actually e.g. y0x0 and also y0x1 should have been connected beforehand by an AND gate before the input, which one has not done here, since it is trivial.

The solution becomes clear if you take this into account :

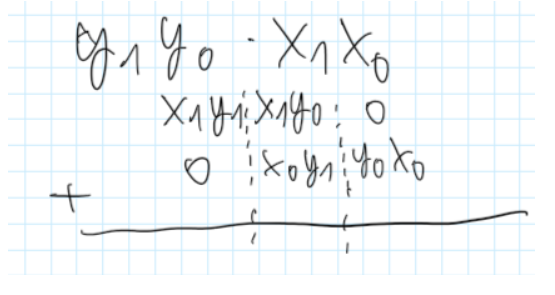
to make clear the solution

Now we have a difficult task. I have to do the same but for: z=y_1 * x * 2 y_0 * x

Also we have to make the solution here:

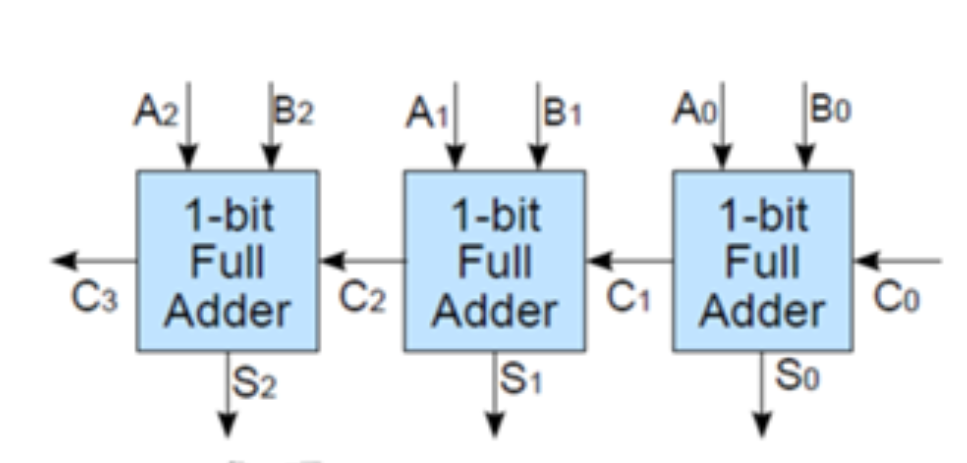
given template for the task

But now how?

CodePudding user response：

So you have 3 inputs: x, y0 and y1 (y = 2 * y1 y0).

The result of y1 * x * 2 y0 * x needs 2 outputs: o0 and o1 (o = 2 * o1 o0).

o1: x and y1
o0: x and y0

The higher bit is only influenced by y1 and x because y1 * x * 2 can only be 0 or 2 and then it doesn't matter if y0 * x is 0 or 1. The lower bit is only influenced by x and y0.

This is just calculating o = x * y with x being a 1 bit number and y being a 2 bit number.

CodePudding user response：

First the math (hope I did not some silly mistake):

              z2z1z0 = y1y0 * x1x0
(z2<<2   z1<<1   z0) = (y1<<1   y0) * (x1<<1  x0)
(z2<<2   z1<<1   z0) = (y1<<1)*(x1<<1  x0)   y0*(x1<<1  x0)
(z2<<2   z1<<1   z0) = (y1*x1<<2)   (y1*x0<<1)   (y0*x1<<1)   (y0*x0)
(z2<<2   z1<<1   z0) = (x1*y1<<2)   (x0*y1<<1)   (x1*y0<<1)   (x0*y0)

Now just separate to individual bits (do not forget to pass carry to the next additions using 1bit full adder). The 1bit multiplication is the same as AND gate and bitshift is just bit position of result so:

(z0) = (x0 AND y0)
(z1) = (x0 AND y1)   (x1 AND y0)
(z2) = (x1 AND y1)   cy(z1)

And circuit:

As you can see you do not even need full adder (non need for input carry) and also you need just 2 of them...

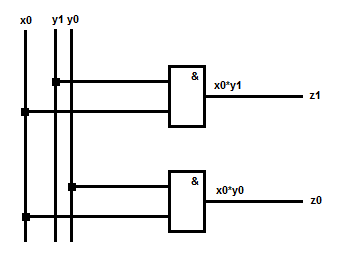
Now your variation is 1*2 bits multiplier so x1=0 so:

(z0) = (x0 AND y0)
(z1) = (x0 AND y1)

so simply:

nothing difficult at all (its just multiplying 2 bit number with 0 or 1 so no carry nor additions...)