I'm plotting several scatter plots with X/Y data. The problem is that, in order to compare the plots, the X/Y axes need to be aligned. I can do this manually but would definitely prefer an automatic solution.
For illustration, I use here one data set from which I want to plot two subsets (in reality though I have two or more completely independent data sets, each with their own time line!) The dataset as a whole is given below.
First plot:
ggplot(df[1:100,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"), name = "time (ms)")
stat_density2d()
The second plot:
ggplot(df[100:200,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"), name = "time (ms)")
stat_density2d()
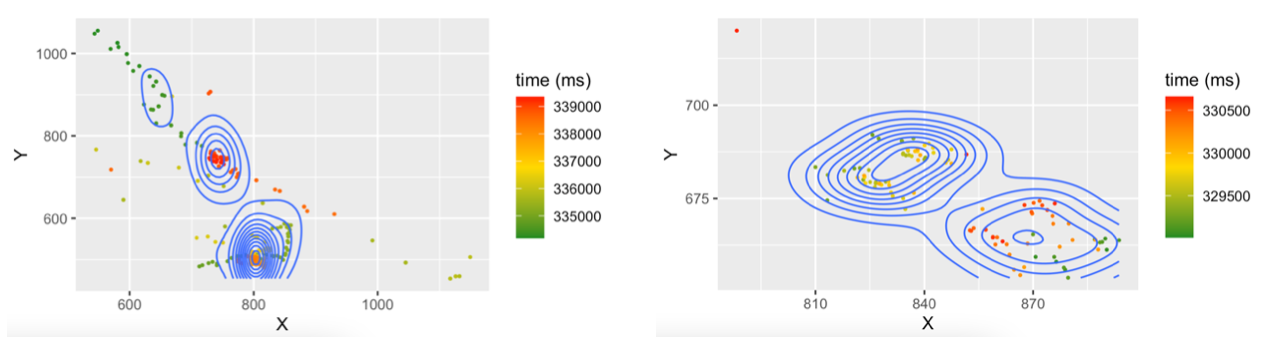
The result:
As can be seen the X/Y axes cover different ranges. How can they be aligned? (And if I may add a second question: how can the two plots be produced in one go and shown immediately side-by-side?)
EDIT:
I've found a solution to the second question - using the package cowplot - so only the question of how to align the X/Y axes of two independent data sets remains to be answered.
library(cowplot)
a <- ggplot(df[1:100,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"), name = "time (ms)")
stat_density2d()
b <- ggplot(df[100:200,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"), name = "time (ms)")
stat_density2d()
plot_grid(a, b)
Data:
df <- structure(list(X = c(886.995, 876.414, 890.29, 870.686, 889.886,
878.858, 893.737, 875.862, 889.03, 878.506, 888.412, 879.659,
869.97, 813.237, 825.718, 820.695, 833.845, 809.99, 827.442,
822.203, 833.764, 813.335, 836.974, 823.124, 840.259, 829.392,
839.988, 817.891, 834.928, 826.655, 834.157, 824.684, 834.119,
826.621, 835.76, 825.053, 835.486, 826.374, 836.49, 834.75, 846.584,
834.155, 847.473, 831.293, 842.564, 830.842, 842.428, 828.199,
841.25, 823.716, 838.123, 823.475, 840.047, 830.131, 845.919,
821.53, 835.386, 830.319, 837.443, 827.744, 838.258, 837.11,
847.505, 827.565, 838.85, 823.371, 838.15, 856.02, 887.157, 867.535,
887.932, 864.748, 877.356, 866.45, 880.88, 863.509, 879.835,
868.479, 875.554, 862.731, 875.356, 859.63, 869.753, 860.095,
871.778, 853.611, 870.142, 852.563, 869.566, 858.956, 872.494,
852.913, 873.889, 856.914, 867.625, 858.928, 876.012, 861.61,
851.618, 788.261, 798.379, 777.557, 798.956, 777.083, 801.887,
778.075, 798.864, 785.822, 799.679, 781.541, 795.737, 785.299,
795.836, 792.412, 799.156, 776.022, 792.404, 787.949, 781.935,
793.567, 771.902, 707.73, 779.717, 788.547, 767.614, 792.656,
774.669, 817.467, 808.79, 821.175, 804.167, 817.827, 804.583,
819.402, 806.682, 818.105, 809.101, 820.088, 795.661, 817.472,
806.363, 817.635, 803.629, 813.491, 800.27, 800.459, 758.664,
785.968, 772.512, 781.696, 769.386, 792.597, 778.636, 793.8,
779.889, 797.779, 777.738, 799.166, 785.231, 795.49, 783.717,
798.131, 786.995, 795.558, 783.907, 798.121, 792.489, 801.123,
793.859, 802.535, 796.445, 800.297, 783.966, 796.06, 774.731,
779.655, 710.941, 721.324, 690.261, 726.259, 664.783, 706.26,
653.884, 699.744, 669.978, 725.24, 711.67, 753.881, 756.447,
795.456, 795.915, 870.223, 855.74, 880.141, 873.236, 901.025,
899.759, 916.765, 915.548, 941.198), Y = c(664.026, 658.045,
661.254, 659.364, 664.259, 655.926, 663.828, 659.352, 663.331,
656.485, 663.223, 653.781, 665.414, 674.523, 692.033, 683.056,
690.348, 683.422, 691.038, 683.172, 690.431, 681.307, 691.108,
679.978, 685.968, 679.486, 685.47, 682.479, 686.535, 679.308,
687.094, 682.646, 686.844, 679.004, 686.636, 679.37, 687.812,
677.968, 686.345, 672.169, 685.389, 675.053, 688.141, 675.668,
687.256, 676.59, 688.574, 678.659, 689.709, 679.089, 687.647,
680.711, 689.211, 679.563, 684.627, 680.587, 688.103, 678.541,
687.672, 678.981, 685.274, 676.507, 684.368, 678.961, 686.621,
681.139, 688.232, 672.178, 663.962, 656.615, 661.313, 655.927,
662.064, 654.477, 663.896, 659.962, 668.294, 662.895, 668.242,
662.718, 670.333, 662.663, 670.956, 664.628, 674.369, 667.075,
673.834, 666.489, 671.39, 664.739, 673.173, 666.36, 671.923,
666.652, 673.249, 664.564, 673.67, 663.489, 686.796, 719.946,
721.271, 721.361, 722.227, 723.032, 721.333, 721.793, 721.419,
723.948, 724.301, 722.893, 723.387, 722.16, 722.367, 720.927,
725.513, 723.396, 726.414, 722.724, 726.956, 730.555, 728.354,
784.936, 729.929, 730.318, 732.103, 730.996, 727.628, 713.195,
708.602, 711.194, 708.453, 713.616, 711.269, 715.176, 709.092,
716.382, 707.973, 715.003, 712.65, 716.613, 708.856, 717.138,
711.883, 717.754, 712.86, 726.009, 738.927, 741.762, 736.506,
741.965, 738.143, 741.771, 736.247, 740.68, 736.025, 738.213,
733.757, 736.281, 731.712, 737.712, 732.11, 738.117, 731.557,
740.61, 732.95, 736.509, 730.86, 734.704, 726.97, 731.913, 724.131,
732.462, 730.361, 738.381, 732.796, 736.228, 738.229, 746.993,
739.654, 734.988, 735.721, 734.151, 725.623, 732.994, 721.506,
718.839, 702.851, 705.922, 693.595, 690.521, 677.954, 667.812,
643.589, 647.281, 630.427, 631.522, 615.858, 621.84, 607.178,
609.407), starttime_ms = c(329011, 329028, 329045, 329061, 329078,
329095, 329111, 329128, 329145, 329161, 329178, 329195, 329211,
329228, 329245, 329261, 329278, 329295, 329311, 329328, 329345,
329361, 329378, 329395, 329411, 329428, 329445, 329461, 329478,
329495, 329511, 329528, 329545, 329561, 329578, 329595, 329611,
329628, 329645, 329661, 329678, 329695, 329711, 329728, 329745,
329761, 329778, 329795, 329811, 329828, 329845, 329861, 329878,
329895, 329911, 329928, 329945, 329961, 329978, 329995, 330011,
330028, 330045, 330061, 330078, 330095, 330111, 330128, 330145,
330161, 330178, 330195, 330211, 330228, 330245, 330261, 330278,
330295, 330311, 330328, 330345, 330361, 330378, 330395, 330411,
330428, 330445, 330461, 330478, 330495, 330511, 330528, 330545,
330561, 330578, 330595, 330611, 330628, 330645, 330661, 330678,
330695, 330711, 330728, 330745, 330761, 330778, 330795, 330811,
330828, 330845, 330861, 330878, 330895, 330911, 330928, 330945,
330961, 330995, 331011, 331028, 331045, 331061, 331078, 331095,
331111, 331128, 331145, 331161, 331178, 331195, 331211, 331228,
331245, 331261, 331278, 331295, 331311, 331328, 331345, 331361,
331378, 331395, 331411, 331428, 331445, 331461, 331478, 331495,
331511, 331528, 331545, 331561, 331578, 331595, 331611, 331628,
331645, 331661, 331678, 331695, 331711, 331728, 331745, 331761,
331778, 331795, 331811, 331828, 331845, 331861, 331878, 331895,
331911, 331928, 331945, 331961, 331978, 331995, 332011, 332028,
332045, 332061, 332078, 332095, 332111, 332128, 332145, 332161,
332178, 332195, 332211, 332228, 332245, 332261, 332278, 332295,
332311, 332328, 332345)), row.names = c(42488L, 42491L, 42493L,
42497L, 42499L, 42502L, 42504L, 42507L, 42509L, 42512L, 42514L,
42517L, 42519L, 42522L, 42524L, 42527L, 42529L, 42532L, 42534L,
42537L, 42539L, 42542L, 42544L, 42547L, 42549L, 42552L, 42554L,
42557L, 42559L, 42562L, 42564L, 42567L, 42569L, 42572L, 42574L,
42577L, 42579L, 42582L, 42584L, 42587L, 42589L, 42592L, 42594L,
42597L, 42599L, 42602L, 42604L, 42607L, 42609L, 42612L, 42614L,
42618L, 42620L, 42623L, 42625L, 42628L, 42630L, 42634L, 42636L,
42640L, 42642L, 42646L, 42648L, 42651L, 42653L, 42656L, 42658L,
42661L, 42663L, 42666L, 42668L, 42671L, 42673L, 42676L, 42678L,
42681L, 42683L, 42686L, 42688L, 42691L, 42693L, 42696L, 42698L,
42701L, 42703L, 42706L, 42708L, 42711L, 42713L, 42716L, 42718L,
42721L, 42723L, 42726L, 42728L, 42731L, 42733L, 42736L, 42738L,
42742L, 42744L, 42748L, 42750L, 42754L, 42756L, 42759L, 42761L,
42764L, 42766L, 42769L, 42771L, 42774L, 42776L, 42779L, 42781L,
42784L, 42786L, 42789L, 42794L, 42796L, 42799L, 42801L, 42805L,
42807L, 42811L, 42813L, 42816L, 42818L, 42821L, 42823L, 42826L,
42828L, 42831L, 42833L, 42837L, 42839L, 42842L, 42844L, 42847L,
42849L, 42852L, 42854L, 42857L, 42859L, 42862L, 42864L, 42867L,
42869L, 42872L, 42874L, 42877L, 42879L, 42883L, 42885L, 42888L,
42890L, 42893L, 42895L, 42898L, 42900L, 42903L, 42905L, 42908L,
42910L, 42913L, 42915L, 42918L, 42920L, 42923L, 42925L, 42928L,
42930L, 42933L, 42935L, 42938L, 42940L, 42943L, 42945L, 42948L,
42950L, 42953L, 42955L, 42958L, 42960L, 42963L, 42965L, 42968L,
42970L, 42973L, 42975L, 42978L, 42980L, 42983L, 42985L, 42988L,
42990L, 42993L, 42995L, 42998L, 43000L), class = "data.frame")
CodePudding user response:
Here's one method. Start by storing the plots:
library(ggplot2)
p1 <- ggplot(df[1:100,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"),
name = "time (ms)")
stat_density2d()
p2 <- ggplot(df[100:200,], aes(x=X, y= Y, color=starttime_ms))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"),
name = "time (ms)")
stat_density2d()
Now get the combined x and y axis limits, with pretty breaks, and assign them to each plot:
xbreaks <- pretty(c(layer_data(p1)$x, layer_data(p2)$x))
ybreaks <- pretty(c(layer_data(p1)$y, layer_data(p2)$y))
p1 <- p1 scale_x_continuous(breaks = xbreaks, limits = range(xbreaks))
scale_y_continuous(breaks = ybreaks, limits = range(ybreaks))
p2 <- p2 scale_x_continuous(breaks = xbreaks, limits = range(xbreaks))
scale_y_continuous(breaks = ybreaks, limits = range(ybreaks))
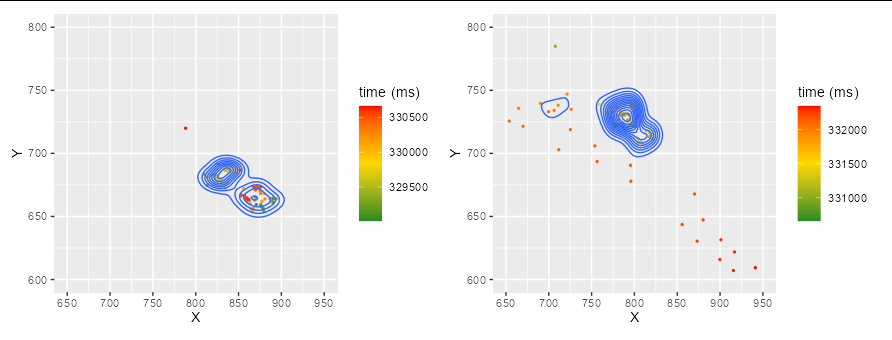
Both plots will now have the same x and y axis. To plot them together on the same page, we simply use the patchwork package:
library(patchwork)
p1 p2
CodePudding user response:
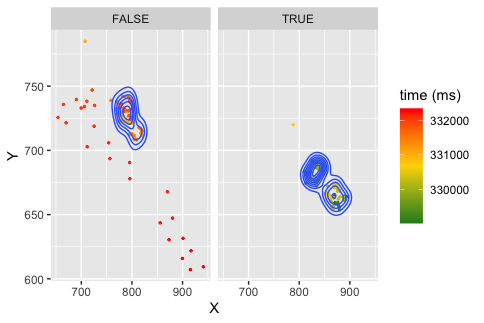
As @PaulStaffordAllen suggests, facet_wrap is the way to go. To use it, you need to add a column to your data that defines the facets.
df %>%
mutate(group=row_number() <= 100) %>%
ggplot(aes(x=X, y= Y, color=starttime_ms, group=group))
geom_point(size = 0.5)
scale_color_gradientn(colors = c("forestgreen", "gold", "red"), name = "time (ms)")
stat_density2d()
facet_wrap(vars(group))
The group=group in the aes() call should calculate statustics (ie the density and colour, within facets, but this plot does not match your separate graphs. I'm not sufficiently familiar with your data to know why that might be. But I notice your colour scales are different between the two plots as well as the axes...