Question.

Create a function drawparabolicshot.m that represents the parabolic shot in 3D knowing that the function has as input the angles O and phi, according to the following expressions:

x=vo*cos(O)*cos(phi)*t,
y=vo*cos(O)*sin(phi)*t, and
z=vo*sin(O)*t-(g/2)*t^2. 

At the moment of representing the function, use plot3 and pause to see how it draws the parabolic trajectory, having fixed previously xlim, ylim and zlim.

Attempt.

function dibujatiroparabolico(phi, O)

vo=100;      %example of vo
g=9.8;        
tmax=(2*vo*sin(O))/(g);
i=1;

for t=linspace(0,tmax)
x(i)=vo*cos(phi)*cos(O)*t;
y(i)=vo*cos(O)*sin(phi)*t;
z(i)=vo*sin(O)*t-(g/2)*t.^2;
i=i 1;
hold on
pause on
plot3(x,y,z)
end

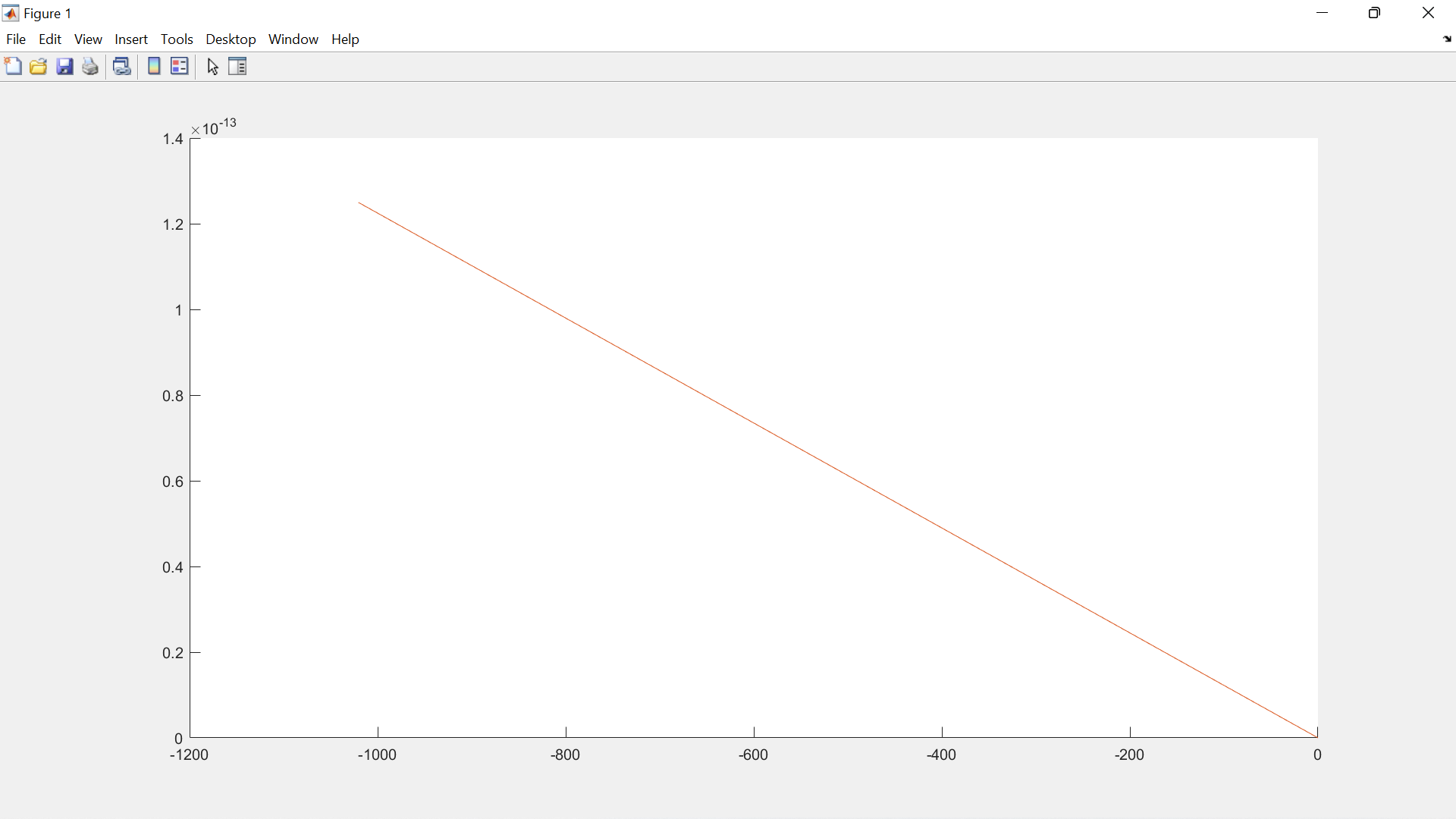
Issue. But it plots a straight line, without showing how it builds and in 2 dimensions even though I used plot3.

What happens when I plot it with examples of phi=pi and O=pi/4:

New Edit.

function dibujatiroparabolico(phi, O)

vo=100;
g=9.8;
tmax=(2*vo*sin(O))./(g);
i=1;

for t=linspace(0,tmax)
x(i)=vo*cos(phi)*cos(O)*t;
y(i)=vo*cos(O)*sin(phi)*t;
z(i)=vo*sin(O)*t-(g/2)*t.^2;
i=i 1;
pause(0.1)
plot3(x,y,z)
xlim([0 tmax*vo*cos(O)*cos(phi)])
ylim([0 tmax*vo*cos(O)*sin(phi)])
zlim([0 vo*sin(O)*(tmax/2)-(g/2)*(tmax/2).^2])
hold on
end

CodePudding user response：

The code you provided do not work for me because cos(phi) is -1 when phi = pi. xlim() wants the limits in the order [min mix], so I corrected your code with xlim(sort([0 tmaxvocos(O)*cos(phi)])). This should be robust to any values of phi and O.

When running this code, I get an animation of the "projectile" flying across the plotting window, with fixed limits.

dibujatiroparabolico(pi, pi/4)

function dibujatiroparabolico(phi, O)

vo=100;
g=9.8;
tmax=(2*vo*sin(O))./(g);
i=1;

    for t=linspace(0,tmax)
        x(i)=vo*cos(phi)*cos(O)*t;
        y(i)=vo*cos(O)*sin(phi)*t;
        z(i)=vo*sin(O)*t-(g/2)*t.^2;
        i=i 1;
        plot3(x,y,z)
        xlim(sort([0 tmax*vo*cos(O)*cos(phi)]))
        ylim(sort([0 tmax*vo*cos(O)*sin(phi)]))
        zlim(sort([0 vo*sin(O)*(tmax/2)-(g/2)*(tmax/2).^2]))
        pause(0.1)
        hold on
    end
end