I have a m by n matrix in matlab and want to find the indices (row, column) of each antidiagonal elements. For example for a 4x3 matrix, I would like to have the following indices:

antidiag1 = (1,1)
antidiag2 = (2,1) , (1,2)
antidiag3 = (3,1) , (2,2), (1,3)
antidiag4 = (4,1) , (3,2), (2,3)
antidiag5 = (4,2) , (3,3)
antidiag3 = (4,3) 

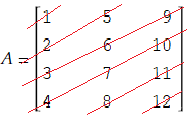
in the above example (m,n)=(row, column). To show what I mean by anti-diagonal elements see the below matrix in which red lines are anti-diagonals

How to find the indices?

CodePudding user response：

The simplest solution to extract the elements is to mirror the matrix horizontally, then find the regular diagonals:

out = diag( flip(in, 2), k );

k here is 0 for the main diagonal, positive for diagonals above the main, and negative for those below, see diag.

To find the indices themselves is a bit more complex. You’d start with a loop to generate candidate pairs, then figure out which pairs are valid:

• The first pair is i=1-k, j=n, with n the width of the matrix and k the desired diagonal.
• Then you iteratively subtract 1 from j and add 1 to i, until j is 1.
• Finally you remove the pairs where i is smaller than 1 or larger than m, the height of the matrix.

This process doesn’t really require a loop, the loop process can be vectorized. Still, it’s easier to describe this way.

In code we could write that as follows (untested!):

[m,n] = size(A);
i = (1:n)-k;
j = n:-1:1;
invalid = (i < 1) | (i > m);
i(invalid) = [];
j(invalid) = [];

CodePudding user response：

The following script is a solution to this question and works well for square and rectangular 2D matrices

clear all;close all;clc

A1=randi([-10 10],3,4)

sz1=size(A1)
        
nA2=reshape([1:1:prod(sz1)],sz1)

nd=sum(sz1)     % amount diagonals

C1={}   % init result cell

for k=-floor(nd/2):1:floor(nd/2)

    a2 = diag( flip(nA2, 2), k )
    [row,col]=ind2sub(sz1,a2)
    C1={C1{:} [row col]}

end

C1(1)=[]  % sought indexes

for k=1:1:size(C1,2)

    C1{k}

end

The solution is contained in cell C1

In MATLAB to read the actual contents of cell elements use curly brackets indexing, like this

 C1{1}
    =
     3     4

 C1{2}
    =
     2     4
     3     3

C1{3}
    =
     1     4
     2     3
     3     2

When indexing with conventional parentheses MATLAB returns the sought elements but inside a cell type

C2(2)

 1×1 cell array
 {2×2 double}

To access individual pairs of solution indexes use the following notation

C1{3}(1,:)
 =
   1     4

C1{3}(2,:)
 =
   2     3

C1{3}(3,:)
 =
   3     2

One can generate the actual variables antidiag1 antidiag2 .. with command evalin