I am having a difficult time understanding and solving recurrence relations. Can someone please help me with this particular one? T(n)=T(n/3) T(2n/3) n

CodePudding user response：

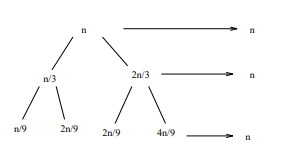
Look at this image:

Which is a recursion tree you can continue.

Also, it's like this one I have found in the URL: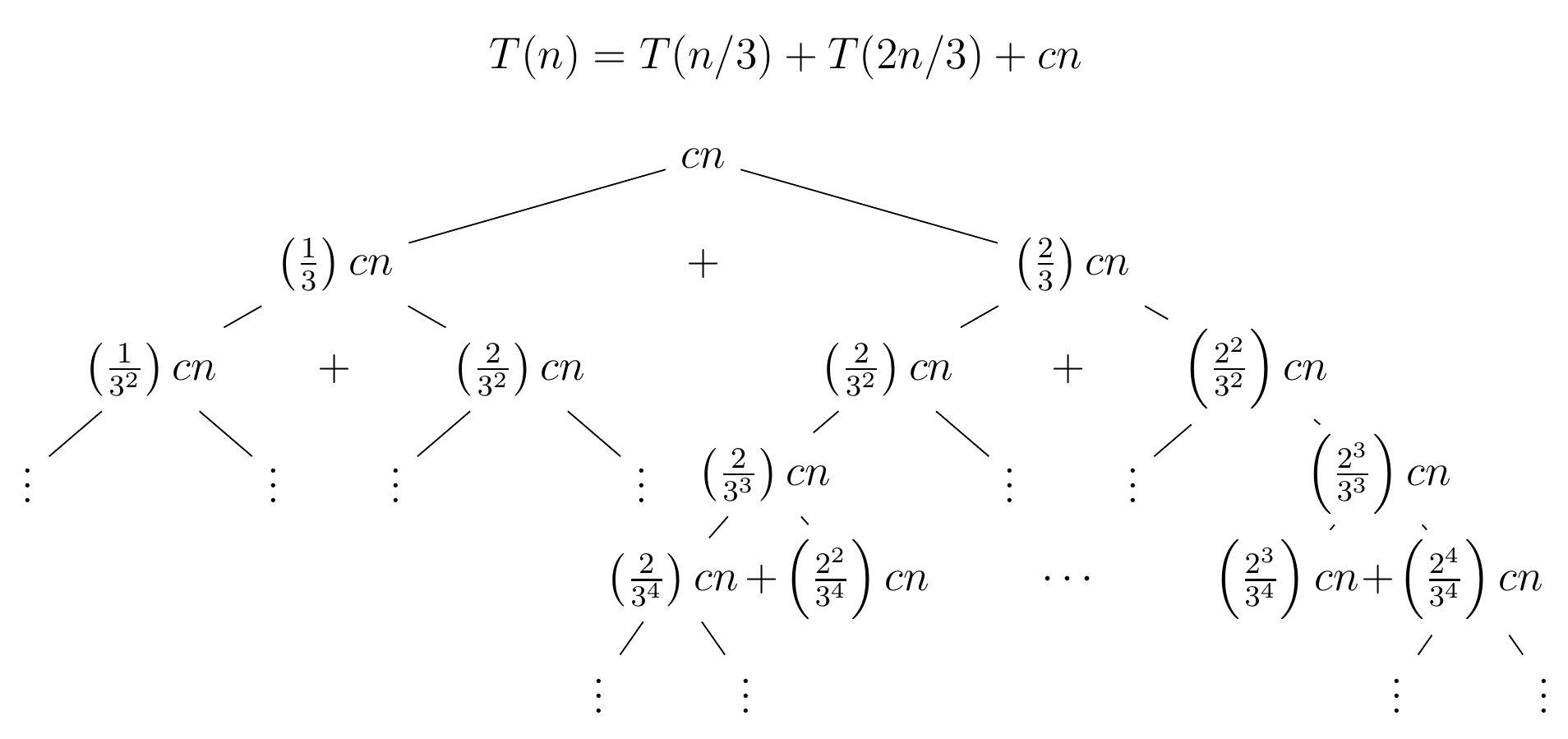

The shortest path to a leaf occurs when we take the heavy branch each time.

Consider k as the height of the tree results: (pow(n*(1/3),k) ≤ 1) meaning k ≥ lg3 n.

The longest path to a leaf occurs when we take the light branch each time.

Consider k as the height of the tree results: (pow(n*(2/3),k) ≤ 1) meaning k ≥ lg3/2 n.

Now look at this image:

This means on any full level, the sum of the additive terms to n.

Now, let's look at what we have.

If you pick height to be

log3 n

The result would be:

1. T(n) ≥ nlog3 n --> T(n) ≥ Ω (nlogn)

If you pick height to be

log3/2 n

The result would be:

2. T(n) ≥ nlog3/2 n --> T(n) ≤ O(nlogn)

And this two (1 & 2) will leads us to T(n) = Θ(nlogn)

Other sources : help