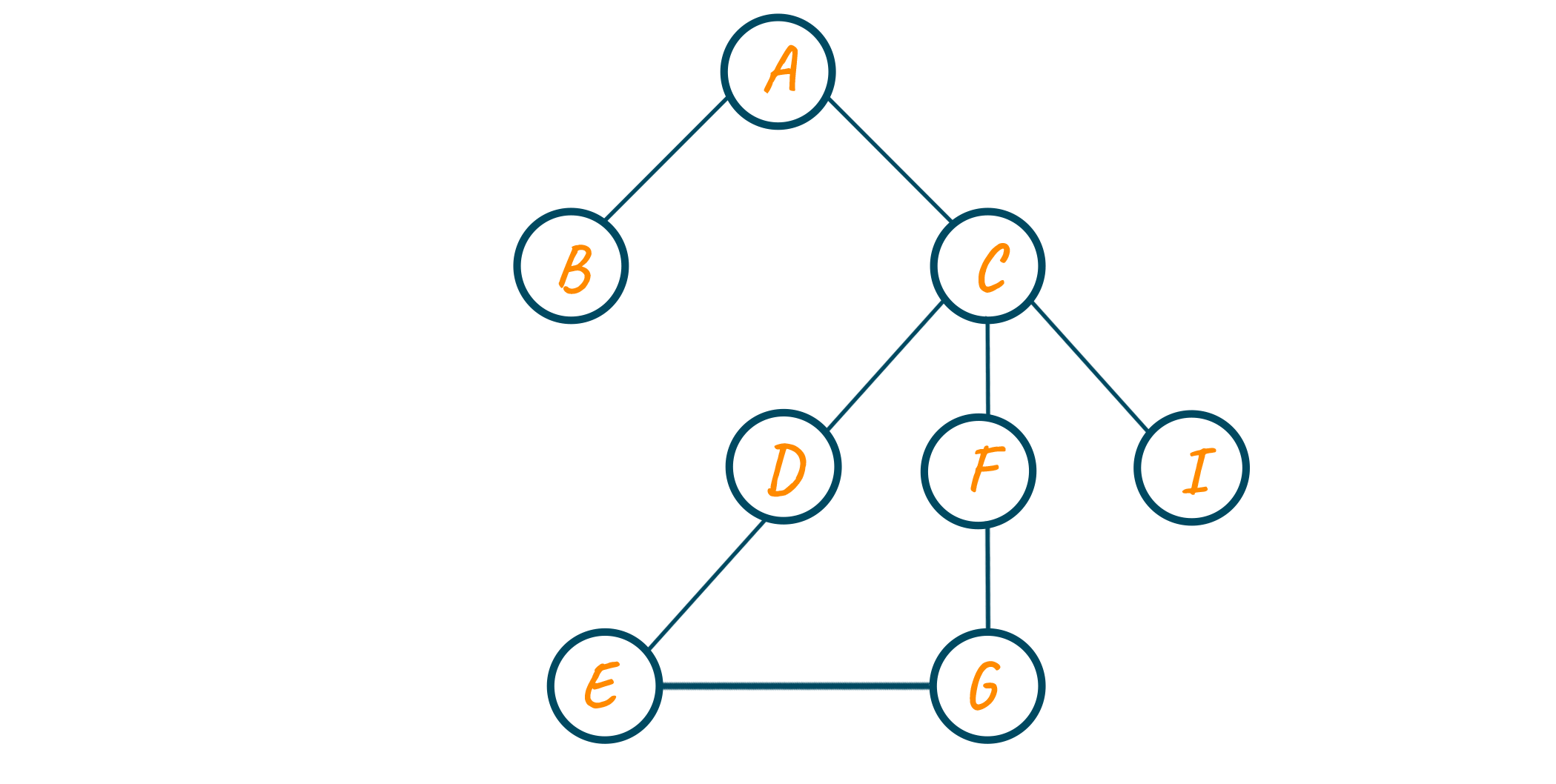
I need to split an undirected graph into minimum number of subpaths (vertices can be repeated, but not edges). Is there any algorithm? How can it be implemented?

For example, for the given graph below, it could be:

BACI, CDEGFC or BACDEGFC, CI

CodePudding user response：

Let's say your graph is connected and has k vertices of odd degree. Then the answer is the max of k/2 and 1. If your graph isn't connected then the same applies to each connected component.

Let's first take the case where there are no vertices of odd degree. Start at any vertex, and keep proceeding to an arbitrary neighbor (along an unused edge) until you get back to the starting vertex. You know you can leave any vertex you can reach because they all have even degree.

If this uses up all edges then you're done. If not, pick a vertex adjacent to an unused edge and repeat. Keep doing this. When done you'll have a number of cycles, say r, and each one will share at least one vertex with another cycle. Next, merge adjacent cycles in the natural way. E.g. in a very simple case we have two triangles that share a vertex: abc and cde, and we finish our procedure with these two small cycles: abca and cdec. We merge these where the meet: abcdeca

a---b
 \ /
  c
 / \
d---e

Now, the issue with vertices of odd degree is that any trail will use up 2 edges adjacent to each vertex in it except the start and end (if different) where it only uses 1. That means that if there are odd vertices, there will be a separate trail for each pair of the same. You can apply the same procedure as before, but always start at an odd-degree vertex. You'll be forced to end at an odd-degree vertex. Merge where you can, but you'll always end up with one trail per pair of odd vertices.