How to start topological sort after a certain element in JavaScript?-CodePudding

I have pieced together this topological sort in JavaScript, and have a graph based on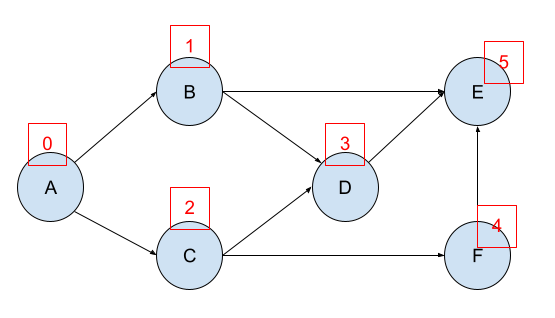

const graph = {
  edges: {
    c: ['d', 'f'],
    d: ['e'],
    f: ['e'],
    a: ['b', 'c'],
    b: ['d', 'e'],
  }
}

// Calcuate the incoming degree of each vertex
const vertices = Object.keys(graph.edges)
const inDegree = {}
for (const v of vertices) {
  const neighbors = graph.edges[v]
  neighbors?.forEach(neighbor => {
    inDegree[neighbor] = inDegree[neighbor]   1 || 1
  })
}

const queue = vertices.filter((v) => !inDegree[v])
const list = []

while (queue.length) {
  const v = queue.shift()
  const neighbors = graph.edges[v]

  list.push(v)

  // adjust the incoming degree of its neighbors
  neighbors?.forEach(neighbor => {
    inDegree[neighbor]--

    if (inDegree[neighbor] === 0) {
      queue.push(neighbor)
    }
  })
}

console.log(list)

99% sure this is a correct implementation of topological sort in JS.

I am interested in doing hot-module reloading, and am interested in simulating updating the relevant nodes in the module graph. So say that d updated. Then we don't care about a, b, or c, they are fine, we only care about updating d and the future node then e, in the order [ d, e ]. We don't care about f because it's not inline with d.

How do I update this topsort function to take a key (the vertex/node), and from that point forward, include the elements, so I get [ d, e ] if I pass d?

Is it as simple as doing list.slice(list.indexOf('d')), or is there more trickiness to the generic/robust solution?

I don't think that is correct because if I did it for module b, we should only have to update [ b, d, e ], but my solution includes c, which is incorrect. Not sure how to go around that.

CodePudding user response：

First you need a priority queue. I'll just borrow Efficient way to implement Priority Queue in Javascript? for this answer.

And now

const vertexPosition = {};
for (let [index, value] of list.entries()) {
  vertexPosition[value] = index;
}

function fromVertex (vertex) {
  let answer = [];
  seen = {vertex: 1};
  let heap = [];
  MinHeap.push(heap, [vertexPosition[vertex], vertex]);

  while (0 < heap.length) {
    let [position, nextVertex] = MinHeap.pop(heap);
    answer.push(nextVertex);
    graph.edges[nextVertex]?.forEach(futureVertex => {
      if (! seen[futureVertex]) {
        seen[futureVertex] = 1;
        MinHeap.push(heap, [vertexPosition[futureVertex], futureVertex]);
      }
    })
  }

  return answer;
}

And now fromVertex('b') gives us [ 'b', 'd', 'e' ]. (Different from what you expected because not having c also means we don't need f.)

CodePudding user response：

Here's another means of accomplishing the task. In short, the algorithm performs a depth first search, tracking the priority (akin to depth) of each node. If, due to multiple paths, the node is encountered again, the priority is reset to the new higher priority, pushing the execution sequence of the node into the proper sequence...

nodes = {
  c: ['d', 'f'],
  d: ['e'],
  f: ['e'],
  a: ['b', 'c'],
  b: ['d', 'e']
};
  
function updateChain( list, node ) {
  
  function traversenode( node, priority ) {
    if ( ( result[ node ] ?? -1 ) < priority ) {
      result[ node ] = priority;
      for ( let child of list[ node ] ?? [] ) {
        traversenode( child, priority   1 );
      }
    }
  }
  
  result = {};
  traversenode( node, 0 );
  return result;
}

console.log( 'b --> ', updateChain( nodes, 'b' ) );

console.log( 'a --> ', updateChain( nodes, 'a' ) );

Note that the other benefit of this technique is that it allows for determination of concurrent processing. That is, all nodes having the same priority can be updated concurrently, assuming of course no underlying dependencies...