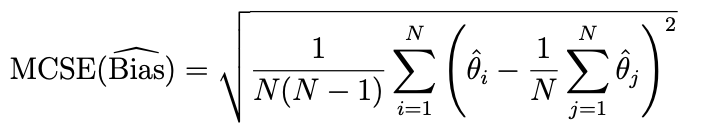The result of Monte Carlo standard error in my code could be wrong in R-CodePudding

I try to compute the Monte Carlo standard error of my estimators. I first got my estimators based on the following repetition of Monte Carlo simulation:

library(VGAM)

# Log-likelihood function of Gumbel distribution
ll_fn <- function(par, z, m){
  mu <- par[1]
  sigma <- par[2]
  -m * log(sigma) - sum((z - mu)/sigma) - sum(exp(-((z - mu)/sigma)))
}

set.seed(101)
N <- 500
#sample size 20
MLE <- replicate(N, {
  x <- rgumbel(20, loc = 0, scale = 1)
  m <- length(x)
  fit <- optim(
    par = c(1, 1),
    fn = ll_fn, z = x, m = m,
    hessian = TRUE, control = list(fnscale = -1)
  )
  fit$par
})

I want to get Bias of estimators.

Bias_mle<-rowMeans(MLE - c(0, 1))
#0.02428035 -0.04154635

And the MCSE of bias is that

So my code is as follows but the results are weird...

MCSE_bias_mle_mu<-sqrt((1/(N*(N-1)))*sum((MLE[1,]-mean(MLE[1,]))^2))
#[1] 0.01081287
MCSE_bias_mle_sigma<-sqrt((1/(N*(N-1)))*sum((MLE[2,]-mean(MLE[2,]))^2))
#[1] 0.007556727

CodePudding user response：

You should follow the definition of MCSE of bias (theta in the formula refers to the estimated parameter, i.e., MLE)

> MCSE_bias_mle <- sqrt(2 * rowSums((MLE - rowMeans(MLE))^2) / choose(N, 2))

> MCSE_bias_mle
[1] 0.02162574 0.01511345

where the 1st and 2nd values are for mu and sigma, respectively