Quick Sort - How to apply recursive and get output-CodePudding

I am working on a school exercise on Quick Sort. I have succeded to do the first exercise which is

Challenge
Given an array 'array' and a number 'p' in the first cell in the array, can you partition the array so that all elements greater than 'p' is to the right of it and all the numbers smaller than 'p' are to it's left? For example, if given the following as input:

4 5 3 9 1 The first number 4 is the pivot, so you should put the smaller numbers to the left, and the larger to the right, and output:

3 1 4 5 9 The array should otherwise remain in the same order.

Can you write code to partition an array?

Example p partition([4, 5, 3, 9, 1])
=> [3, 1, 4, 5, 9]

My code for the above in ruby is

def partition(array)
  # write your code here
  pivot = array.shift()
  base = [pivot]
  left = []
  right = []
  array.each { |e| if e < pivot
                  left.push(e)
               else
                  right.push(e)
               end
          }
  left   base   right
end

p partition([4, 5, 3, 9, 1])
# => [3, 1, 4, 5, 9]

The Challenge for which I am raising this Question is

The function should output like this

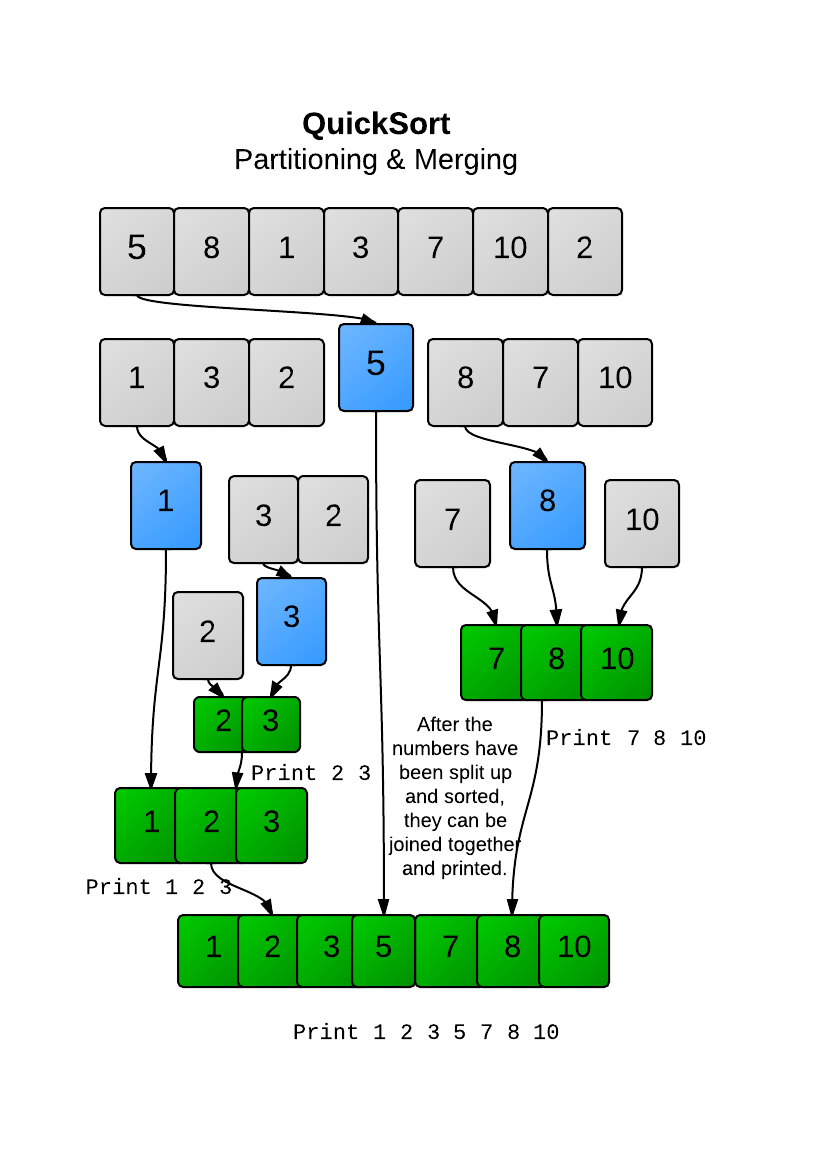
p some_function_name([5, 8, 1, 3, 7, 10, 2])
# => 2 3
#    1 2 3
#    7 8 10
#    1 2 3 5 7 8 10

I am trying for the last 36hrs how to apply the partition code above recursively on this challenge. During my 36hrs of research on the Quick Sort algorithm, I can make the code to give the result of a sorted array, but this challenge is asking to provide prints at certain conditions which I am not able to achieve.

Any help is much appreciated.

This one tried for pivot at end

def partition(array)
    # write your code here
    pivot = array[-1]
    i = -1
    j = 0
    while j < array.length-1
        if array[j] < pivot
            i  = 1
            array[i], array[j] = array[j], array[i]
        end
        j  = 1
    end
    array.insert(i 1, array.pop)
    puts index = i 1
    puts (array.take index).join(' ')
    puts (array.drop index 1).join(' ')
end

partition([5, 8, 1, 3, 7, 10, 2])

this one, I am not able to find a condition for terminating recursive function

def partition(array)
    # write your code here
    pivot = array.shift()
    base = [pivot]
    left = []
    right = []
    array.each { |e| if e < pivot
                    left.push(e)
                 else
                    right.push(e)
                 end
            }
    left   base   right
    if left.length < 2
      return
    end
    partition(left)
  end

p partition([5, 8, 1, 3, 7, 10, 2])
p partition([1, 3, 2])
p partition([8, 7, 10])

CodePudding user response：

It's not clear to my why you want partition to be recursive. There is no real natural way to make it recursive in a simple way. You can introduce a recursive helper method, but I don't see that as an improvement. partition really doesn't need to be more complicated than this:

def partition(array, pivot)
  return [], [] if array.empty?

  array.partition(&pivot.method(:>))
end

If you absolutely must, you can make it recursive like this:

def partition(...) = partition_rec(...)

private def partition_rec(array, pivot, left = [], right = [])
  return left, right if array.empty?

  first = array.first
  rest = array.drop(1)

  if first < pivot
    partition_rec(rest, pivot, left   [first], right)
  else
    partition_rec(rest, pivot, left, right   [first])
  end
end

With this partition in place, we can easily write our quicksort:

def quicksort(array)
  return array if array.length < 2

  pivot = array.first
  left, right = partition(array.drop(1), pivot)

  quicksort(left)   [pivot]   quicksort(right)
end

Now, all we need to do is to also print the result at each recursive call. A simple way to do that would be with Kernel#p, which returns its argument, so we can just insert it without changing the return value:

def quicksort(array)
  return array if array.length < 2

  pivot = array.first
  left, right = partition(array.drop(1), pivot)

  p quicksort(left)   [pivot]   quicksort(right)
end

If we need to replicate the exact format of the string as given in the question, then we should use Kernel#puts instead:

def quicksort(array)
  return array if array.length < 2

  pivot = array.first
  left, right = partition(array.drop(1), pivot)

  (quicksort(left)   [pivot]   quicksort(right)).tap do |result|
    puts result.join(' ')
  end
end

Note that there is a big no-no in your code. Here, you are modifying the argument passed into partition:

array.shift()

Same here:

array.insert(i 1, array.pop)

You must not, ever, mutate an argument. In fact, you should avoid mutation at all, as much as possible. The only thing you are allowed to mutate is yourself, i.e. self. But even then, you should be careful.