Laplace correction with conditions for smoothing-CodePudding

I have a data (user_data) that represent the number of examples in each class (here we have 5 classes), for example in first row, 16 represent 16 samples in class 1 for user1, 15 represent that there is 15 samples belong to class 2 for user 1, ect.

user_data = np.array([
    [16, 15, 14, 10, 0],
    [0, 13, 6, 15, 21],
    [12, 29, 1, 12, 1],
    [0, 0, 0, 0, 55]])

I calculated the probability vector of each users by using method of Peter Flash’s book

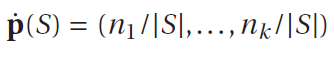
probability vector

where |S|=55 and the number of examples in S of class Ci is denoted ni.

Output:

array([[0.29090909, 0.27272727, 0.25454545, 0.18181818, 0.        ],
       [0.        , 0.23636364, 0.10909091, 0.27272727, 0.38181818],
       [0.21818182, 0.52727273, 0.01818182, 0.21818182, 0.01818182],
       [0.        , 0.        , 0.        , 0.        , 1.        ]])

I used the following method to smooth all these frequencies to avoid issues with extreme values (0 or 1) by using Laplace smoothing where k=2.

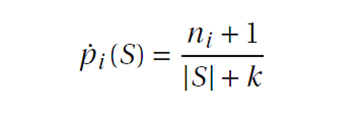
Laplace smoothing

Output:

array([[0.29824561, 0.28070175, 0.26315789, 0.19298246, 0.01754386],
       [0.01754386, 0.24561404, 0.12280702, 0.28070175, 0.38596491],
       [0.22807018, 0.52631579, 0.03508772, 0.22807018, 0.03508772],
       [0.01754386, 0.01754386, 0.01754386, 0.01754386, 0.98245614]])

But I want to smooth only extreme values (0 or 1) in this data, red Square represent extreme value:

extreme value only smoothed

So, only extreme values (0 and 1) are smoothed

Expected output:

CodePudding user response：

I have noticed that your smoothing approach will cause P > 1, you are to clip or normalize the values later on:

probs = user_data/55
alpha = (user_data 1)/(55 2)
extreme_values_mask = (probs == 0) | (probs == 1)
probs[extreme_values_mask] = alpha[extreme_values_mask]

Result:

array([[0.29090909, 0.27272727, 0.25454545, 0.18181818, 0.01754386],
       [0.01754386, 0.23636364, 0.10909091, 0.27272727, 0.38181818],
       [0.21818182, 0.52727273, 0.01818182, 0.21818182, 0.01818182],
       [0.01754386, 0.01754386, 0.01754386, 0.01754386, 0.98245614]])

Extension:

# Scale by sum.
probs /= probs.sum(1).reshape((-1, 1))
print(probs)
print(probs.sum(1))

[[0.28589342 0.26802508 0.25015674 0.17868339 0.01724138]
 [0.01724138 0.2322884  0.10721003 0.26802508 0.37523511]
 [0.21818182 0.52727273 0.01818182 0.21818182 0.01818182]
 [0.01666667 0.01666667 0.01666667 0.01666667 0.93333333]]
[1. 1. 1. 1.]

CodePudding user response：

You can use np.where, which follows the format np.where(condition, value if condition is true, value if condition is false) – feel free to read the documentation here.

For example:

S = 55
k = 2

np.where((user_data/S == 0) | (user_data/S == 1), (user_data 1)/(S   k), user_data/S)

Result:

array([[0.29090909, 0.27272727, 0.25454545, 0.18181818, 0.01754386],
       [0.01754386, 0.23636364, 0.10909091, 0.27272727, 0.38181818],
       [0.21818182, 0.52727273, 0.01818182, 0.21818182, 0.01818182],
       [0.01754386, 0.01754386, 0.01754386, 0.01754386, 0.98245614]])