How to correctly plot a linear regression on a log10 scale?-CodePudding

I am plotting two lists of data against each other, namely freq and data. Freq stands for frequency, and data are the numeric observations for each frequency.

In the next step, I apply the ordinary linear least-squared regression between freq and data, using stats.linregress on the logarithmic scale. My aim is applying the linear regression inside the log-log scale, not on the normal scale.

Before doing so, I transform both freq and data into np.log10, since I plan to plot a straight linear regression line on the logarithmic scale, using plt.loglog.

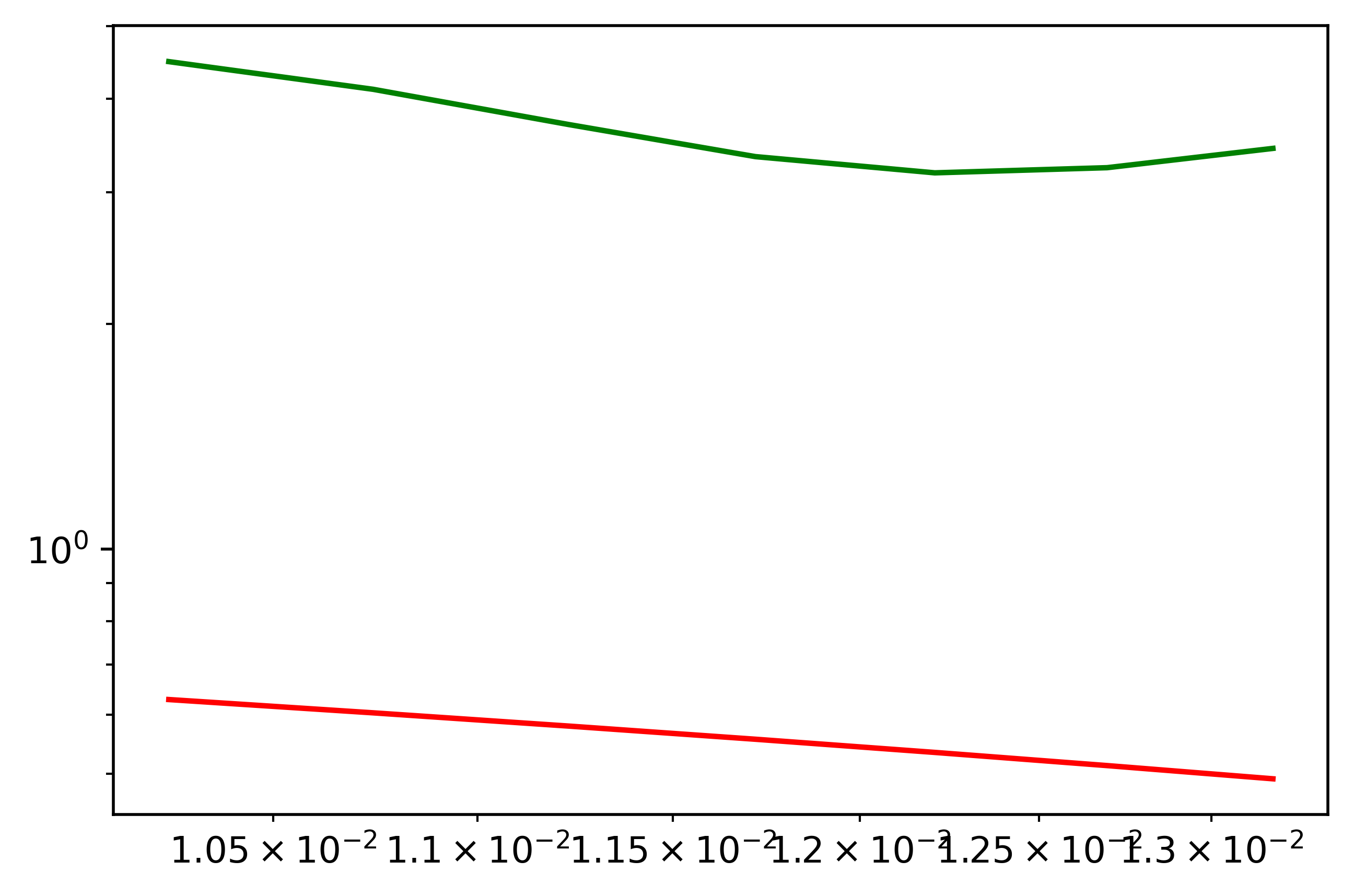
Problem: The problem is that the regression line, plotted in red color, is plotted far from the actual data, plotted in green color. I assume that there is a problem in combination with plt.loglog in my code, hence the visual distance between the green data and the red regression line. How can I fix this problem, so that the regression line plots on top of the actual data?

Here is my reproducible code:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Data
freq = [0.0102539, 0.0107422, 0.0112305, 0.0117188, 0.012207, 0.0126953,
        0.0131836]
data = [4.48575,  4.11893,  3.69591,  3.34766,  3.18452,  3.23554,  3.43357]

# Plot log10 of freq vs. data
plt.loglog(freq, data, c="green")

# Linear regression
log_freq = np.log10(freq)
log_data = np.log10(data)

reg = stats.linregress(log_freq, log_data)
slope = reg[0]
intercept = reg[1]

plt.plot(freq, slope*log_freq   intercept, color="red")

And here is a screenshot of the code’s result:

CodePudding user response：

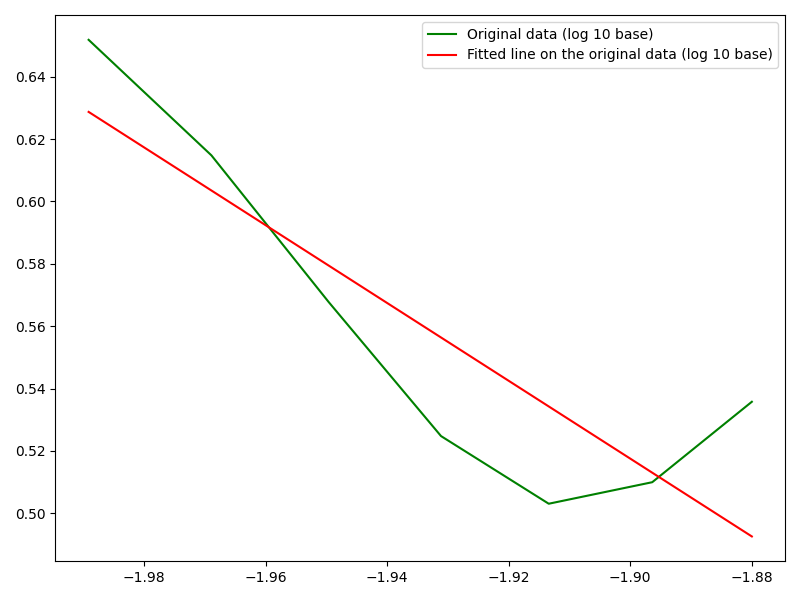
You can convert your data sets to log base 10 first, then do linear regression and plot them accordingly.

Note that after the log transformation, the numbers inlog_freq will all be negative; therefore x-axis cannot be log-scaled.

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Data
freq = np.array([0.0102539, 0.0107422, 0.0112305, 0.0117188, 0.012207, 0.0126953,
                 0.0131836])
data = np.array([4.48575, 4.11893, 3.69591, 3.34766, 3.18452, 3.23554, 3.43357])

# transform date to log base 10
log_freq = np.log10(freq)
log_data = np.log10(data)

# Plot freq vs. data
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(log_freq, log_data, c="green", label='Original data (log 10 base)')

# Linear regression
reg = stats.linregress(log_freq, log_data)

# Plot fitted freq vs. data
ax.plot(log_freq, reg.slope * log_freq   reg.intercept, color="red",
        label='Fitted line on the original data (log 10 base)')

plt.legend()
plt.tight_layout()
plt.show()

References:

First of all, I question the necessity of log-log axes, because the ranges of the data, or at least the ranges of the data that you've shown us, are limited on both coordinates.

In the code below, I have

computed the logarithms in base 10 of your arrays,
used the formulas for linear regression but using the logarithms of data to obtain the equation of a straight line:
y = a b·x
in, so to say, the logarithmic space.

Because a straight line in log-space corresponds, in data-space, to a power law, y = pow(10, a)·pow(x, b), I have plotted

the original data, in log-log, and
the power law, also in log-log,

obtaining a straight line in the log-log representation.

import matplotlib.pyplot as plt
from math import log10
freq = [.0102539, .0107422, .0112305, .0117188, .012207, .0126953, .0131836]
data = [4.48575, 4.11893, 3.69591, 3.34766, 3.18452, 3.23554, 3.43357]
n = len(x)

lx, ly = [[log10(V) for V in v] for v in (freq, data)]
sum_x = sum(x for x in lx)
sum_y = sum(y for y in ly)
sum_x2 = sum(x**2 for x in lx)
sum_y2 = sum(y**2 for y in ly)
sum_xy = sum(x*y for x, y in zip(lx, ly))

# coefficients of a straight line "y = a   b x" in log-log space
b = (n*sum_xy - sum_x*sum_y)/(n*sum_x2-sum_x**2)
a = (sum_y - b*sum_x)/n

plt.loglog(freq, data)
A = pow(10, a)
plt.loglog(freq, [A*pow(x, b) for x in freq])