Continuous fraction approximation of pi-CodePudding

While studying for Matlab, I came up with this problem: given an integer $1\leq d\leq 15$ find the smallest $p,q$(positive integers) such that $|\frac{p}{q}-\pi|\leq 10^{-d}$.

So here's my attempt: I first thought that I need to bound p,q in order to create loops, so I put as input data some $M,N$ upper bounds for $p,q$ respectively. So here is my algorithm:

       M=input('Give an upper bound for p:')
       N=input('Give an upper bound for q:')
       d=input('Give a positive integer between 1 and 15:')

       for q=1:N
       for p=1:M
       if abs(pi-p/q)<=10^(-d)
       break
       end
       end
       end

What is wrong about it? Thank you in advance.

CodePudding user response：

The problem lies in the the way you chose to terminate the for loops: break only stops the inner loop. Try this code instead, and check the value of p and q at which the execution stops:

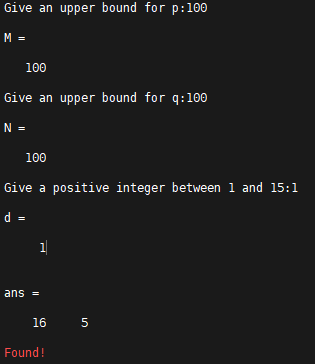
 M=input('Give an upper bound for p:')
 N=input('Give an upper bound for q:')
 d=input('Give a positive integer between 1 and 15:')

 for q=1:N
 for p=1:M
   if abs(pi-p/q)<=10^(-d)
     [p,q]
     error('Found!') % Arrest the program when condition is met
 end
 end
 end

which gives the following output:

Of course, there are better ways of capturing all the possible pairs of integers that meet the condition (e.g. by using disp instead of error). That goes beyond the scope of this answer, but I shall provide a couple of examples here:

clear; clc;

M=input('Give an upper bound for p:')
N=input('Give an upper bound for q:')
d=input('Give a positive integer between 1 and 15:')

pairs = []; % p,q pairs are stored here
k = 1; % counter

for q=1:N
    for p=1:M
        if abs(pi-p/q)<=10^(-d)
            pairs(k,1) = p; 
            pairs(k,2) = q;
            k = k   1; % increment the counter
        end
    end
end

The script above will end quietly: the (p,q) pairs will be stored in the pair matrix.

The following one will print directly the pairs:

clear; clc;

M=input('Give an upper bound for p:')
N=input('Give an upper bound for q:')
d=input('Give a positive integer between 1 and 15:')

for q=1:N
    for p=1:M
        if abs(pi-p/q)<=10^(-d)
            out = sprintf("(%d, %d)", p,q);
            disp(out);
        end
    end
end

If you are interested in continuous fraction approximations of pi, try rat(pi, Tol) where Tol is the tolerance. Further details here.