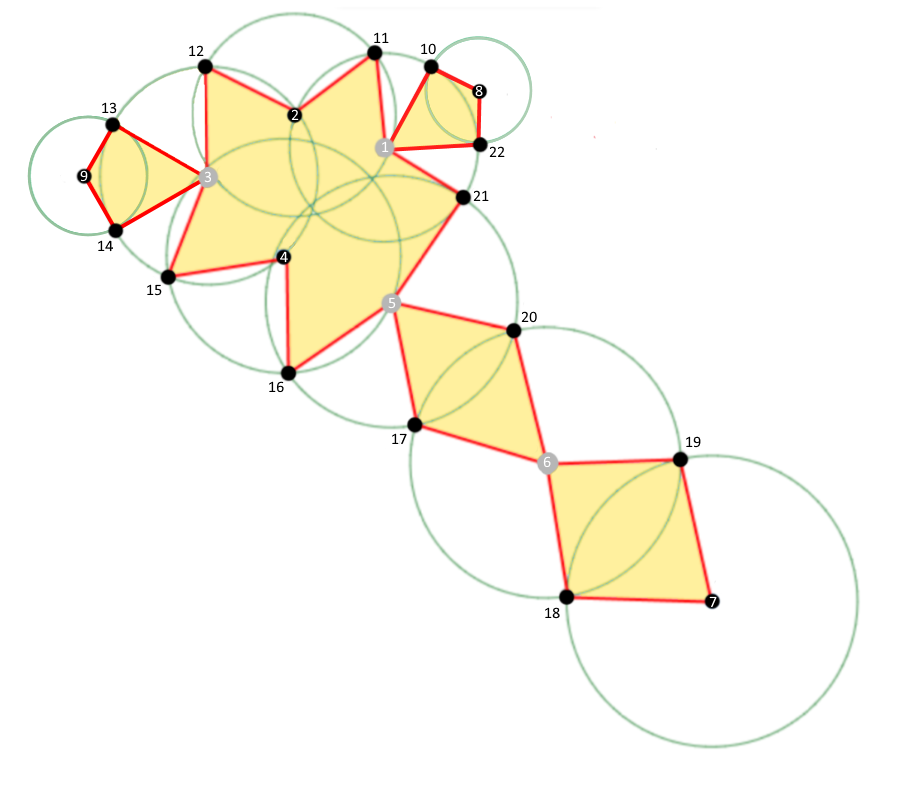
Currently, I have a program (actually two identical programs in python and lua) that generates a graph-structure of numbered nodes (at specific coordinates) and edges as shown in the following image:

The graph is currently stored in a {node:[neighbours]} dictionary/table. As you can see it is a large shape made up of separate polygons joined at different intersection nodes (grey), and these polygons will never overlap (although I do not think this matters if we're only considering the graph edges).

I am looking for a way to calculate the area of the shaded region, and to do that, I need to be able to separate the shape into the individual polygons (or somehow traverse the outer edge of the shape, but that would require taking vertex positions into account, and I think it can be done using the graph alone).

The algorithm I require would have the following output for the example image:

[
  [1,22,8,10],
  [1,11,2,12,3,15,4,16,5,21],
  [3,12,9,14],
  [5,17,6,20],
  [6,18,7,19]
]

Corresponding to the 5 different polygons that make up the shape.

I've been trying to do this for hours and I've got nowhere, other than the fact that the intersection nodes will always have a degree > 2, and all degrees are even.
Any help would be greatly appreciated, in python, lua, pseudocode, or even just the basic steps of the algorithm.

CodePudding user response：

I believe something like this might work:

1. take some start index - let's say 1
2. take the edge that is most on the right (in case of start point this does not matter which one - so let's say 22)
3. proceed until you find a conjunction - store the path. 1 -> 22 -> 8 -> 10 -> 1 (you have your first polygon)
4. repeat step 2. the edge most on the right is 1 -> 11
5. repeat step 3. 1 -> 11 -> 2 -> 12 -> 3
6. take the right edge 3 -> 13 , so branch and continue 3 -> 13 -> 9 -> 14 -> 3 (second polygon)
7. now continue 1 -> 11 -> 2 -> 12 -> 3 as it's not closed, continue to 15 -> 4 -> 16 -> 5
8. etc

CodePudding user response：

Brute force:

- Find enclosing rectangle of all the vertices
- LOOP R over points in a raster covering enclosing rectangle
   - LOOP P over polygons
       - IF R inside P
           ( If overlapping polygons allowed: check that R is not already counted )
           INCREMENT count of covered raster points
- AREA = count * raster increment * raster increment / 4

You can adjust the raster increment to get the best trade off between precision and running time. You will get better results with a compiled language ( e.g. C ) rather than python which is far too slow for this sort of work. )

The best performance ( and therefore the best precision ) requires careful optimization of the code checking if a point is inside a polygon. Here is a description and C code for highly optimized algorithm for this https://ravenspoint.wordpress.com/2010/06/27/in-or-out/