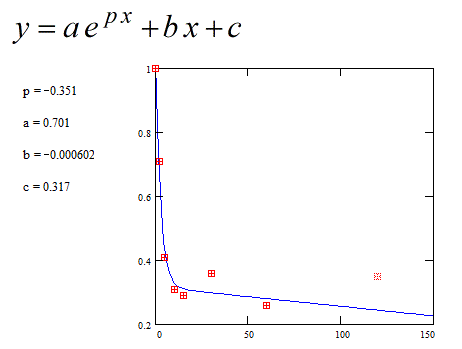
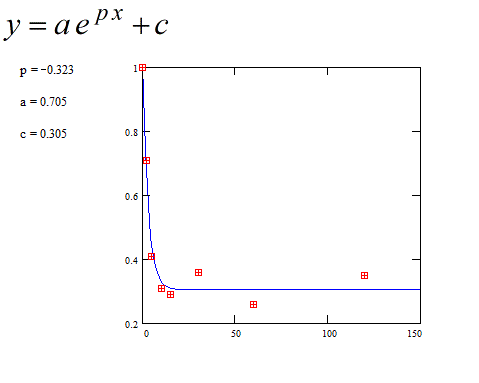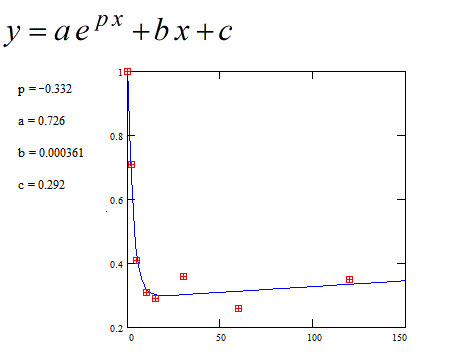I have this set of experimental data:

x_data = np.array([0, 2, 5, 10, 15, 30, 60, 120])
y_data = np.array([1.00, 0.71, 0.41, 0.31, 0.29, 0.36, 0.26, 0.35])

t = np.linspace(min(x_data), max(x_data), 151)

The result is not bad considering the wide scatter on the right part.

Second : Fitting to an exponential function with a linear function (without taking account of the expected decreasing on the right).

The slope of the linear part is very low : 0.000361

But the slope is positive which is not as wanted.

Since the scatter is very large one suspects that the slope of the linear function might be governed mainly by the scatter. In order to check this hypothesis one make the same fitting calculus whitout one point. Taking only the seven first points (that is forgetting the eighth point) the result is :

Now the slope is negative as wanted. But this is an untruthful result.

Of course if some technical reason implies that the slope is necessarily negative one could use a picewise function made of an exponenlial and a linear function. But what is the credibility of such a model ?

This doesn't answer to the question. Neverthelss I hope that this inspection will be of interest.

For information :

The usual nonlinear regression methods are often non convergent in case of large scatter due to the difficulty to set initial values of the parameters sufficienly close to the unknown correct values. In order to avoid the difficulty the above fittings where made with a non usual method which doesn't requires "guessed" initial value. For the principle refer to :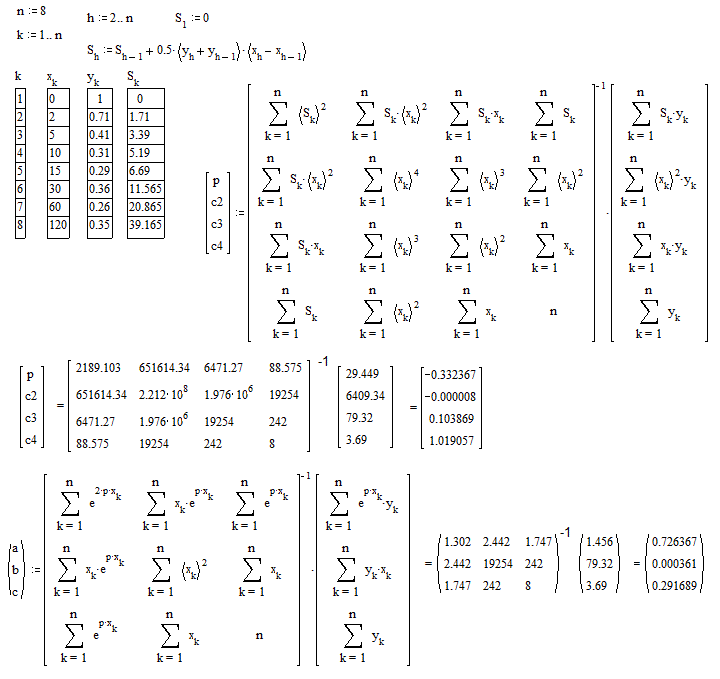

If more accuracy is needed use a nonlinear regression software with the values of p,a,b,c found above as initial values to start the iterative calculus.