I would like to use SQL to solve an algebraic equation for market share solving for the quantity of Product 1 to achieve a target market share.

Data:

Target: 35%

Equation: ([Product 1 Quantity] * [Target]) / (([Product 1 Quantity] * [Target]) ([Product 2] Product 3] [Product 4]))

Let x = Target, A = Product 1 Qty, B = sum(Product 2 Quantity, Product 3 Quantity, Product 4 Quantity)

Ax/(Ax B) = 0.35 or 300x / (300x   700) = 0.35

1. Simplify:

   3x / 3x 7 = 0.35

2. Multiply both sides by 3x 7:

   3x = 0.35(3x 7)

3. Multiply both sides by 100

   300x = 35(3x 7)

4. Expand 35(3x 7)

   300x = 105x 245

5. Move to left

   195x = 245

6. Solve

   x = 49/39

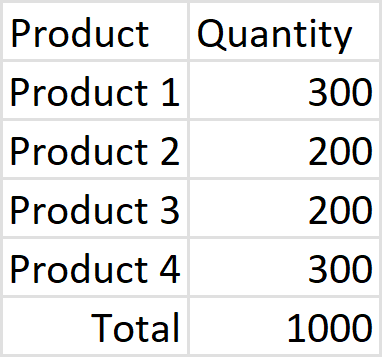
Current: Product 1 has a quantity of 300 of the 1,000 total quantity or 30%. What I am trying to solve, what is the total additional quantity needed of Product 1 to achieve 35%? Keep in mind an increase of Product 1 also increases the total quantity.

How can this be solved using MSSQL? Any other suggestions? Greatly appreciate any help! Thank you.

CodePudding user response：

Here's a slighly different version:

DECLARE @target NUMERIC(9,2) = 0.35
,   @A INT
,   @B INT
,   @TARGET_COEFF NUMERIC(19, 9)

SELECT  @A = MAX(CASE WHEN Product = 'Product1' THEN Quantity END)
,   @B = SUM(CASE WHEN Product <> 'Product1' THEN Quantity END)
FROM
(
    VALUES  (N'Product1', 300)
    ,   (N'Product2', 200)
    ,   (N'Product3', 200)
    ,   (N'Product4', 300)
    ,   (N'Total', 1000)
) t (Product,Quantity)
WHERE   Product <> 'Total'

/*
Ax / (Ax   B) = 0.35

Ax = 0.35 * Ax   B * 0.35

Ax - 0.35Ax = B * 0.35

0.65Ax = B * 0.35

x = B * @target / (( 1 - @target) * A)

*/
SELECT  @TARGET_COEFF = @B * @target / ((1 - @target) * @A)

SELECT  @TARGET_COEFF AS coeff, @A * @TARGET_COEFF AS new_quantity, @A * @TARGET_COEFF - @A AS needed
,   @A * @TARGET_COEFF / (@B   @A * @TARGET_COEFF) AS verification

I included inside the transformation of the equation so you get x by itself as well as some verification. Most important thing is that you transform your equation correctly.

Output:

CodePudding user response：

In order to calculate the minimum amount x needed for a given product quantity a to meet the specified target threshold T (given the sum of the other products' quantity b), you can use the following formula:

x = (Ta - a   Tb) / (1 - T)

The simplest case is for 2 products. For example, if Product A and Product B both have a quantity of 5 (50% each), and you want to see how many more of Product A you need to order to hit 60%, you can calculate it as follows:

x = ((0.6 * 5) - 5   (0.6 * 5)) / (1 - 0.6) = 2.5

So for either product to hit 60%, you'd need to order (just) 2.5 (or realistically, 3).

As you add other products, the equation stays the same: Your b just becomes the sum of the other products' quantities. So for example, if you had 3 products with a quantity of 5 each, you'd use 10 for the value of b.

But how do we translate this into SQL? We can use a windowed sum to compare the total quantity to each product. Then, we can do the calculation in a query (even using a lateral join, or CROSS APPLY in MS SQL syntax) to simplify the equation. For example:

DECLARE @target DECIMAL(18,2) = 0.35;

WITH windowed AS 
(
  SELECT *, SUM(quantity) OVER () * 1.0 AS total 
  FROM products
)
SELECT 
  product
  quantity,
  total,
  quantity / total AS current_percent,
  @target AS target_percent,
  CASE 
    WHEN (quantity / total) < @target 
    THEN ((T * a) - a   (T * b)) / (1 - T)
  END AS needed
FROM windowed
  CROSS APPLY
  (
    SELECT 
      quantity AS a,
      total - quantity AS b,
      @target AS T
  ) eq

working fiddle here.