A compass in the plane, known to rotate an acute Angle a, before and after a coordinate rotation Angle is known,
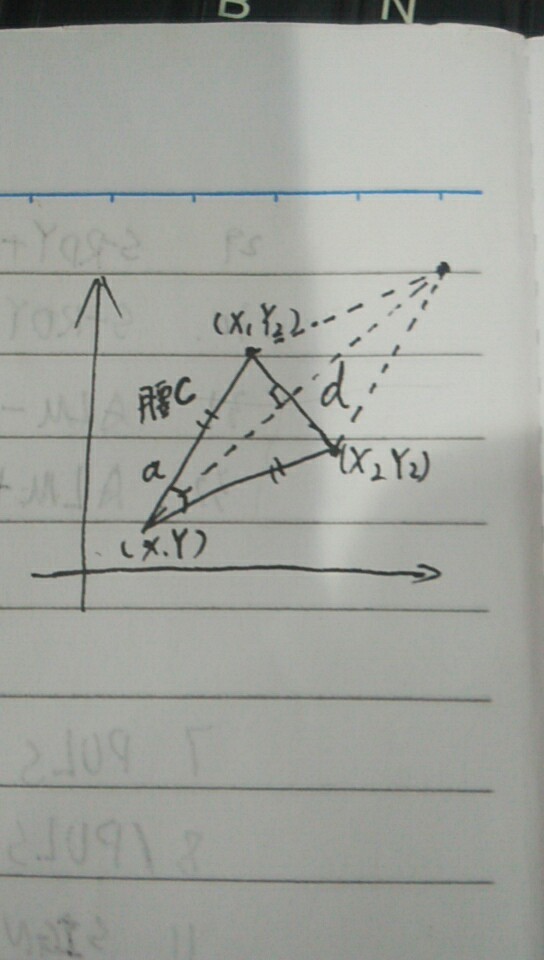
Before (X1, Y1), after turn (X2, Y2), X1, Y1, X2, Y2 are greater than zero, strives for the compass rotation center coordinates (X, Y)?

Feeling such a solution formula out very hard!

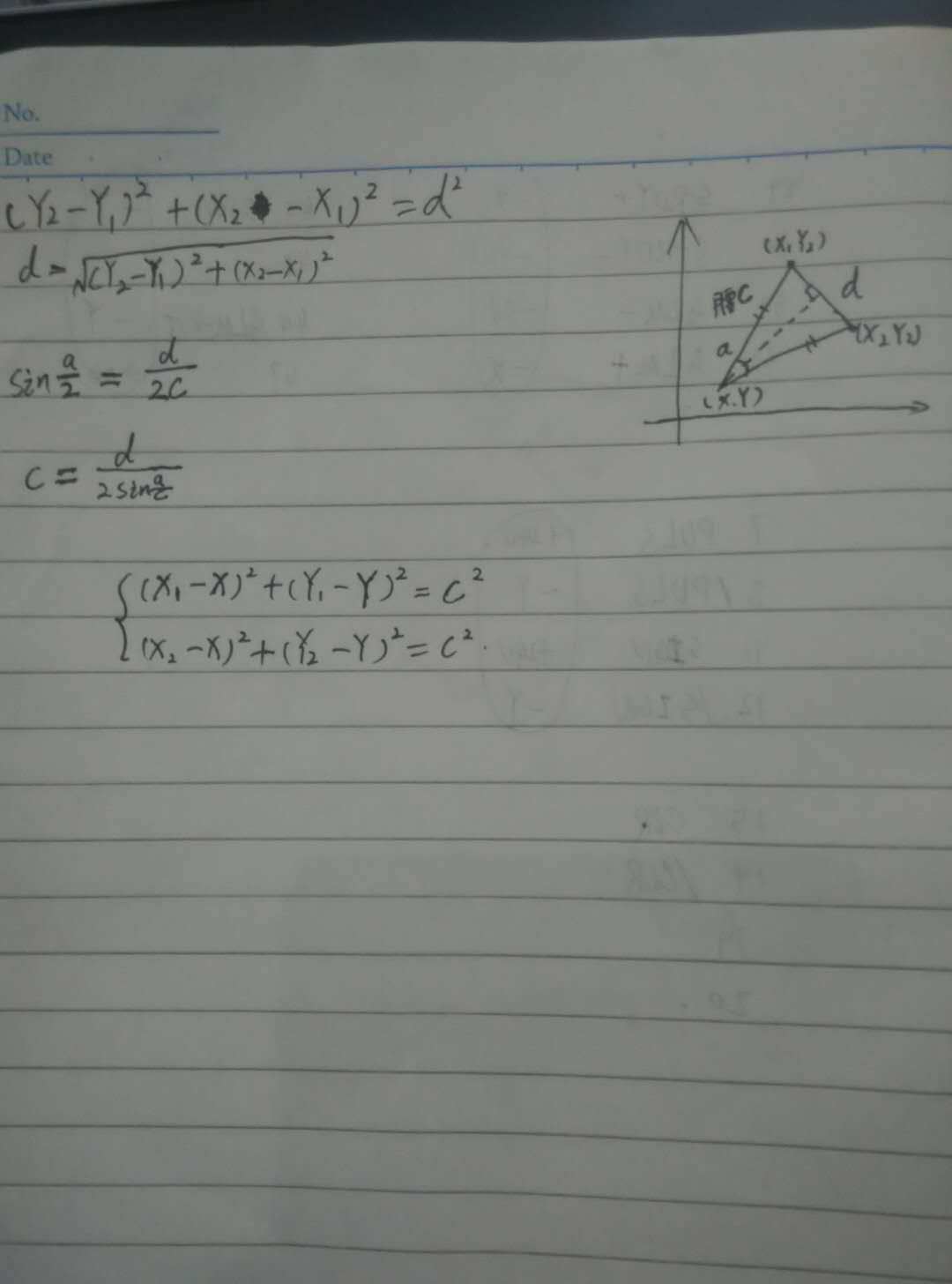
CodePudding user response:

Don't use the Pythagorean theorem, this can seek out all the angles in the figure, also can seek out the length of the all, not complicated with trigonometric functions

CodePudding user response:

Basic math problem!

CodePudding user response:

https://baike.baidu.com/item/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5/3265181? fr=aladdin

CodePudding user response:

Equations out is complicated, can use the tool
Point t
Coordinates (a, b) (c, d)
X, y
Equation:
(x - a) * (x - a) + (y - b) * (y - b)=(x - c) * (x - c) + (y - d) * (y - d)
(x - a) * (x - a) + (y - b) * (y - b) * sin (t/2) * sin (t/2)=((a - c) * (a - c) + (b, d) * (b, d))/4

The results for the
X=(d * (b * (2 * SQRT (d ^ 2 * b * d + c ^ 2-2-2 * a * c + b ^ 2 + a ^ 2) * SQRT (1 - sin (t/2) ^ 2) + a * (2 * sin (t/2) ^ 2-4)) - 2 * b * c * sin (t/2) ^ 2) ^ 2 + d * ((- SQRT (d ^ 2 * b * d + c ^ 2-2-2 * a * c + b ^ 2 + a ^ 2) * SQRT (1 - sin (t/2) ^ 2)) + c * sin (t/2) ^ 2 + a * (2 - sin (t/2) ^ 2)) + b ^ 2 * (a * (2 - sin (t/2) ^ 2) - SQRT (d ^ 2 * b * d + c ^ 2-2-2 * a * c + b ^ 2 + a ^ 2) * SQRT (1 - sin (t/2) ^ 2)) + c * (b ^ 2 * sin (t/2) ^ 2 - a ^ 2 * sin (t/2) ^ 2) + c ^ 3 * sin (t/2) ^ 2 - a * c ^ 2 * sin (t/2) ^ 2 + a ^ 3 * sin (t/2) ^ 2)/(2 * c ^ 2 * sin (t/2) ^ 2-4 * a * c * sin (t/2) ^ a ^ 2 + 2 * 2 * sin (t/2) ^ 2 + 2 * d ^ 2-4 * b * d * b ^ 2 + 2),
y=(d*(c*(sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)-2*a)-a*sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+c^2-b^2+a^2)+b*(a*sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+a^2*(2*sin(t/2)^2-1))+b*c*(a*(2-4*sin(t/2)^2)-sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2))+b*c^2*(2*sin(t/2)^2-1)+d^3-b*d^2+b^3)/(2*c^2*sin(t/2)^2-4*a*c*sin(t/2)^2+2*a^2*sin(t/2)^2+2*d^2-4*b*d+2*b^2),x=(d*(b*(a*(2*sin(t/2)^2-4)-2*sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2))-2*b*c*sin(t/2)^2)+d^2*(sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+c*sin(t/2)^2+a*(2-sin(t/2)^2))+b^2*(sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+a*(2-sin(t/2)^2))+c*(b^2*sin(t/2)^2-a^2*sin(t/2)^2)+c^3*sin(t/2)^2-a*c^2*sin(t/2)^2+a^3*sin(t/2)^2)/(2*c^2*sin(t/2)^2-4*a*c*sin(t/2)^2+2*a^2*sin(t/2)^2+2*d^2-4*b*d+2*b^2),y=(d*(c*((-sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2))-2*a)+a*sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+c^2-b^2+a^2)+b*(a^2*(2*sin(t/2)^2-1)-a*sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2))+b*c*(sqrt(d^2-2*b*d+c^2-2*a*c+b^2+a^2)*sqrt(1-sin(t/2)^2)+a*(2-4*sin(t/2)^2))+b*c^2*(2*sin(t/2)^2-1)+d^3-b*d^2+b^3)/(2*c^2*sin(t/2)^2-4*a*c*sin(t/2)^2+2*a^2*sin(t/2)^2+2*d^2-4*b*d+2*b^2)

The results for the tool automatic computing
Address: https://zh.numberempire.com/equationsolver.php

CodePudding user response:

Under a formula without the parenthesis, change to use tools to try to be

CodePudding user response:

A complete solution: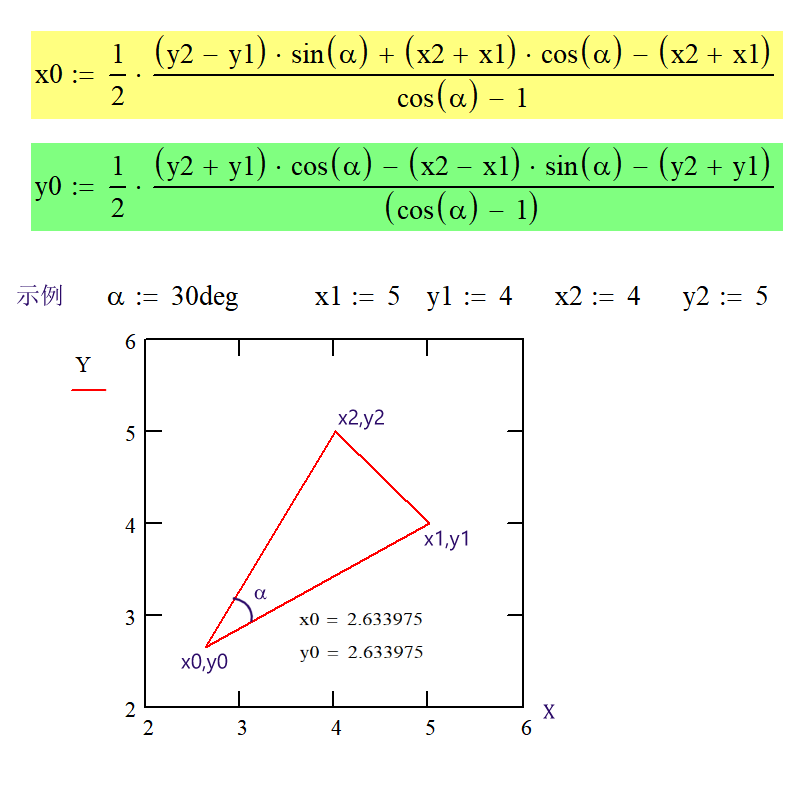

CodePudding user response:

Upstairs posts,

The geometric sketchpad verification results

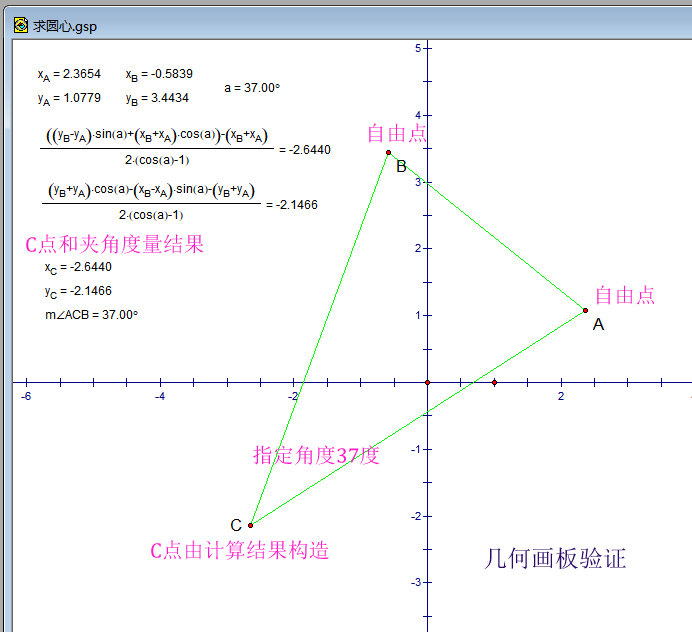
CodePudding user response:

This algorithm is not limited to the first quadrant, if the Angle & lt; 180 degrees, is the center point C is located in the left of the vector AB,

CodePudding user response:

1 in 4 quadrants, 2 points in one quadrant formula has a problem,

CodePudding user response:

CodePudding user response:

In a train of thought is fitting circle algorithm

CodePudding user response:

Feel the 7th floor is no problem