Before this period of matlab was already in the diagonal of covariance matrix and a very small number, in order to prevent the occurrence of covariance matrix, it is the result of the feel is wrong, should not be mixed gaussian probability of less than one? I will post the results below,

 function gp=GaussianPDF (data, u, sigmai) 
% UNTITLED3 shown here on the function of the 
% details is shown here 
[m, n]=size (data); 
U=mean (data, 1); 
Nxt_item (1: m)=0; 
tem_data=https://bbs.csdn.net/topics/data-repmat (u, m, 1); 
Sigmai=sigma (data); 
For I=1: m 
Pre_item=1/SQRT (((2 * PI) ^ n) * abs (det (sigmai) + realmin)); 
Tem_data_t=tem_data (I:) '; 
Nxt_item (I)=exp (0.5 * (tem_data (I, :) * inv (sigmai) * tem_data_t)); 
End 

Gp=pre_item * nxt_item; 

End 

Here is my input and the results

 & gt;> data=https://bbs.csdn.net/topics/[1, 2, 3, 4 and 6, 7,8,9] 

Data=https://bbs.csdn.net/topics/

1 2 3 
4 5 6 
7 8 9 
U=mean (data, 1) 

U=

4 5 6 
> Sigmai=sigma (data) 

Sigmai=

9.0000 9.0000 9.0000 
9.0000 9.0000 9.0000 
9.0000 9.0000 9.0000 

> GaussianPDF (data, u, sigmai) 

Ans=

1.0 e+03 * 

1.4823 2.4439 1.4823 

I don't think this is the right result, but I don't know how to continue

CodePudding user response:

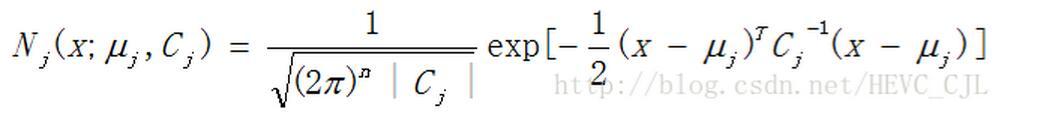
I am the building Lord, is based on the formula

CodePudding user response:

In diagonal covariance matrix and the number of small, prevent the problem of singular matrix, but the result is also very strange, I don't know what's the problem

CodePudding user response:

In opencv function calculated is greater than 1, the building Lord solved

CodePudding user response:

Was true probability density is not equal to the probability formula is given probability density formula can be greater than 1