Bosses, what is the subject of their thinking, I want to define the square on the loop please
CodePudding user response:
The topic request is not clear?
Enter a positive number n, and then judge n how many times have greater than or equal to 10000, 00000, this is how much power of the solution,
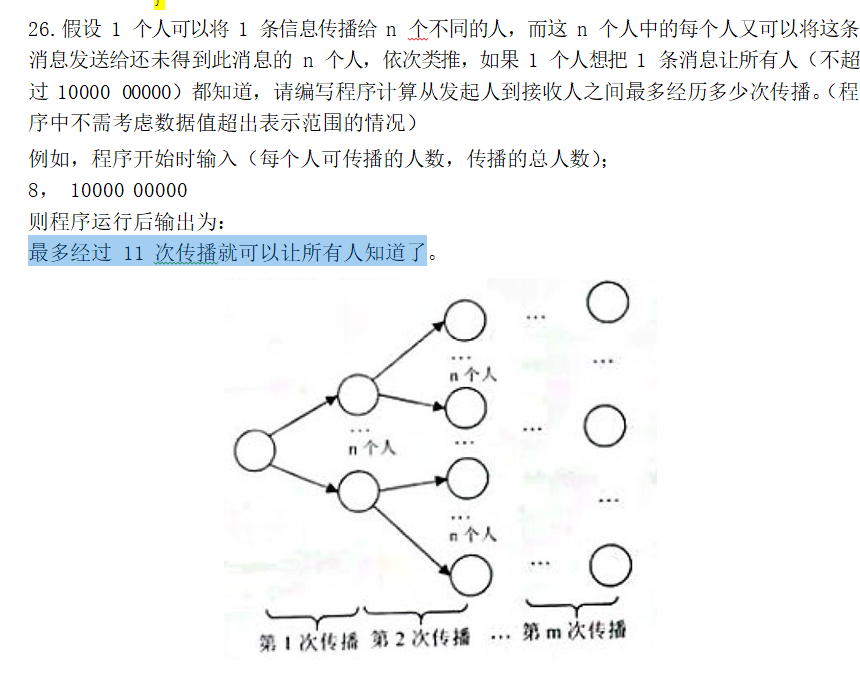
Such as a person up to eight people, to be passed on to 100 people, so,
For the first time, to eight people, that is, 1 of 8 square
Second, the eight everyone again to the other eight people, also is the square of 8 * 8=64=8, only 64 people know at this time, still not meet 100 people, so you need to continue to spread
Third, this 64 people each person to the other eight people, or 64 * 8=512=8 cubic, there are 512 people know, meet 100 people, so you need to spread 3
The code example
Int main () {
Int n, m, p, q;
The scanf (" % d % d ", & amp; N, & amp; M);
For (q=1, p=n; p
Printf (" need to spread % d times ", q);
return 0;
}
CodePudding user response:
reference 1st floor qybao response: the topic request is not clear? CodePudding user response:
With geometric series summation formula: CodePudding user response:
reference movsd reply: 3/f with geometric series summation formula: CodePudding user response:
Ceil mean ceiling