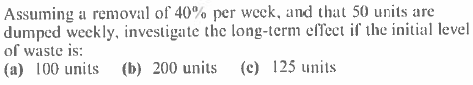How to solve recurrence relations in R-CodePudding

I am well aware that R was designed for statistics and not for recurrence relations, however it would be great to be able to do this.

I am taking Higher Applications of Maths and am given a choice between using excel or R to do the exam with. I am using R for the rest of the exam so I would preferably like to be able to solve the recurrence relation using it as well to avoid me having to switch between the two.

Here is some example questions:

In all of these questions I am trying to find the point where they converge. I am assuming that this will require a recursive function but I am not too sure where to go from there.

Any help would be appreciated.

CodePudding user response：

This type of question can be handled with a simple loop in R. For example, the first question could be tackled by writing the following function:

waste_simulation <- function(initial_value)
{
   units <-initial_value
   units <- c(units, units[1] * 0.6   50)
   
   while(units[length(units)] != units[length(units) - 1]) {
      units <- c(units, units[length(units)] * 0.6   50)
   }
   return(units)
}

This allows you to test each initial starting value:

waste_simulation(100)
#>  [1] 100.0000 110.0000 116.0000 119.6000 121.7600 123.0560 123.8336 124.3002
#>  [9] 124.5801 124.7481 124.8488 124.9093 124.9456 124.9673 124.9804 124.9882
#> [17] 124.9929 124.9958 124.9975 124.9985 124.9991 124.9995 124.9997 124.9998
#> [25] 124.9999 124.9999 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [33] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [41] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [49] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [57] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [65] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
 
waste_simulation(200)
#>  [1] 200.0000 170.0000 152.0000 141.2000 134.7200 130.8320 128.4992 127.0995
#>  [9] 126.2597 125.7558 125.4535 125.2721 125.1633 125.0980 125.0588 125.0353
#> [17] 125.0212 125.0127 125.0076 125.0046 125.0027 125.0016 125.0010 125.0006
#> [25] 125.0004 125.0002 125.0001 125.0001 125.0000 125.0000 125.0000 125.0000
#> [33] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [41] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [49] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [57] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [65] 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000 125.0000
#> [73] 125.0000
 
waste_simulation(125)
#> [1] 125 125

We can see that in all 3 cases the value converges to 125 (which is 50/0.4).

^{Created on 2021-11-02 by the reprex package (v2.0.0)}