How to find the necessary rotation of a rectangle to land on the ellipse-CodePudding

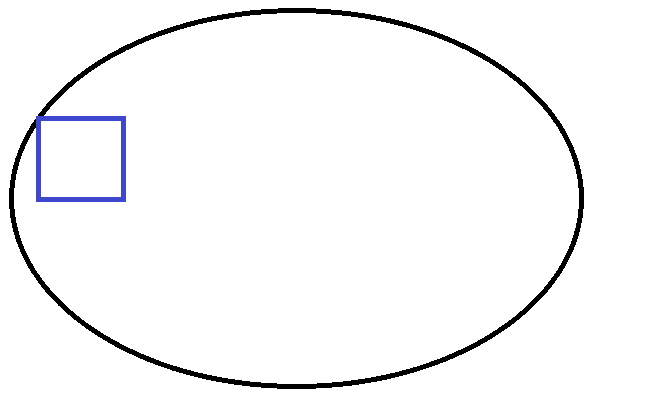
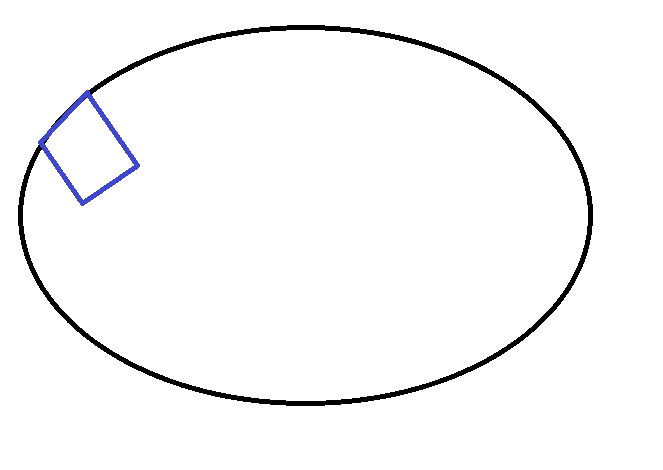
From the upper left point of the rectangle on an eclipse, I would like to know what calculation I have to do to find the necessary angle to apply to my rectangle so that the upper right corner arrives on the ellipse.

I have something like that

and I intend to rotate the right side of the rectangle, so that it arrives on the eclipse.

the information I have :

for the rectangle :

the coordinates(x,y) of the rectangle
the length of each side of the rectangle

for the eclipse :

the spokes
the height and the length

Thank you!

EDIT :

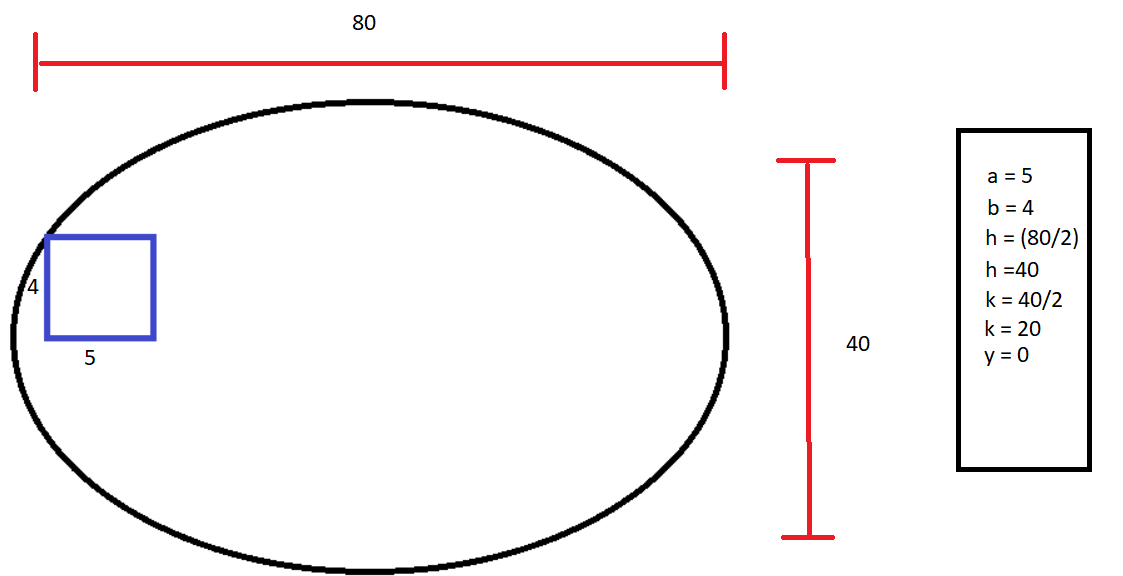
So if i try it, i have to start by determining a, b, h,k. Y is always equal to zero if I understood correctly.

So, to do my example,i added values to my drawing. These values correspond to the lengths and heights of the rectangles and the eclipse. With that I determined the variables necessary for the equation.

here is my drawing :

application of the equation :

(y - k)^2 = b^2(1 - ((x - h) / a)^2)
(0-20)^2 = 4^2(1-((x-40)/5)^2)
400 = 16(1-((x-40)/5)^2)
400 = 16(1-((x-40)/5)^2)

400 = 16(1-(2((x-40)/5)))
... calculate that : 2((x-40)/5)
= x(5/5)-2((x-40)/5) = 0
= x(5)-2((x-40)/5) = 0
= (5x-2x 80)/5 = 0
= (3x 80)/5 = 0
= (3(x) 80)/5 = 0
= (3(x) 3(26.66))/5 = 0
= (3(x 26.66))/5 = 0
= (5/3)((3(x 26.66)/5)) = 0
= (1/3)(3(x 26.66)) = 0
= x 26.66 = 0
x = -26.66
so i replace it in my equation.
400 = 16(1-(-26.66))
400 = 16(1 26.66)
400 = 16(27.66)
400 = 442.56
? = 442.56-400
? = 42.56.

that's what it is to me, but i think it's not the result i expect. Can you edit your answer to help me because I don't know how to get the quadratic formula? Thank you.

CodePudding user response：

First, you need to understand that the ellipse is a geometrical space that can be described by an equation. See more here: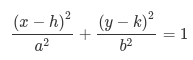

From here you can see that

(y - k)^2 = b^2(1 - ((x - h) / a)^2)

You will get a quadratic equation with two solutions:

y is negative
y is positive

since y is positive in your case, you can make that assumption in your calculations when you determine what y actually is. From then on, you seek the derivative of y in the point where the left-hand top corner of your square touches the ellipse. That will provide the line to which you need to rotate your square. The angle of your square's top side and the line you have found using the derivative is the angle you seek. You can use arccos, arcsin or arctan to get that value, depending on your preference.