Let me explain as best as i can. This is about binary tree using vector.
According to author, the implementation is as follows:

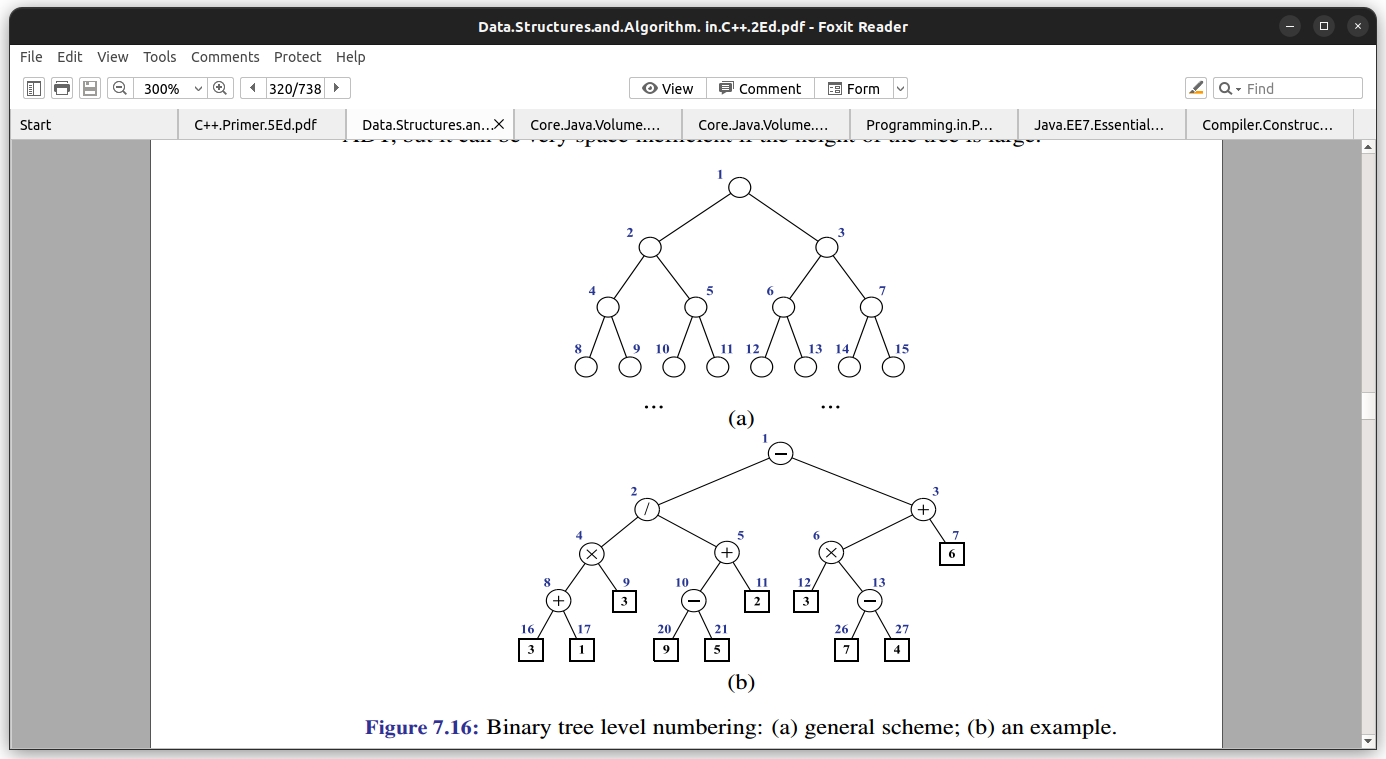
A simple structure for representing a binary tree T is based on a way of numbering the nodes of T. For every node v of T, let f(v) be the integer defined as follows:
• If v is the root of T, then f(v) = 1
• If v is the left child of node u, then f(v) = 2 f(u)
• If v is the right child of node u, then f(v) = 2 f(u) 1
The numbering function f is known as a level numbering of the nodes in a binary tree T, because it numbers the nodes on each level of T in increasing order from left to right, although it may skip some numbers (see figures below).

Let n be the number of nodes of T, and let fM be the maximum value of f(v) over all the nodes of T. The vector S has size N = fM 1, since the element of S at index 0 is not associated with any node of T. Also, S will have, in general, a number of empty elements that do not refer to existing nodes of T. For a tree of height h, N = O(2h). In the worst case, this can be as high as 2^n − 1.

Question:

1. The last statement worst case 2^n-1 does not seem right. Here n=number of nodes. I think he meant 2^h-1 instead of 2^n-1. Example from figure a) height = 4. Worst case space usage (a proper binary tree) then 2^4-1 = 16-1 = 15. Having 2^n -1 means 2^15-1 = 32768-1 = 32767. Does not make sense.

Any insight is appreciated.
Thanks.

CodePudding user response：

The worst case is when the tree is degenerated to a chain from the root, where each node has two children, but at least one of which is always a leaf. When this chain has n nodes, then the height of the tree is n/2. The vector must span all the levels and allocate room for full levels, even though there is in this degenerate tree only one node per level. The size S of the vector will still be O(2^h), but now that in this degenerate case h is O(n/2) = O(n), this makes it O(2ⁿ) in the worst case.

The formula 2^n-1 seems to suggest the author does not have a proper binary tree in mind, and then the above reasoning should be done with a degenerate tree that consists of a single chain where every node has at the most one child.

Example of worst case

Here is an example tree (not a proper tree, but the principle for proper trees is similar):

           1
          /
         2
          \
           5
            \
             11

So n = 4, and h = 3.

The vector however needs to store all the slots where nodes could have been, so something like this:

                     _____ 1 _____
                    /             \
                 __2__          __   __     
                /     \        /       \
                      _5_   
             /   \   /   \   /  \     /   \
                         11

...so the vector has a size of 1 2 4 8 = 15. (Even 16 when we account for the unused slot 0 in the vector)

This illustrates that the size S of the vector is always O(2^h). In this worst case (worst with respect to n, not with respect to h), S is O(2ⁿ).

Example n=6

When n=6, we could have this as a best case:

         1
       /   \
      2     3
     / \     \
    4   5     7

This tree can be represented by a vector of size 8, where the entries at index 0 and index 6 are filled with nulls (unused).

However, for n=6 we could have a worst case ("worst" for the impact on the vector size) when the tree is very unbalanced:

           1
            \
             2
              \
               3
                \
                 4
                  \
                   5
                    \
                     7

Now the tree's height is 5 instead of 2, and the vector needs to put that node 7 in the slot at index 63... S is 64. Remember that the vector spans each complete binary level, which doubles in size at each next level.

So when n is 6, S can be 8, 16, 32, or 64. It depends on the shape of the tree. In each case we have that S=O(2^h). But when we express S in terms of n, then there is variation, and the best case is that S=O(n), while the worst case is S=O(2ⁿ).