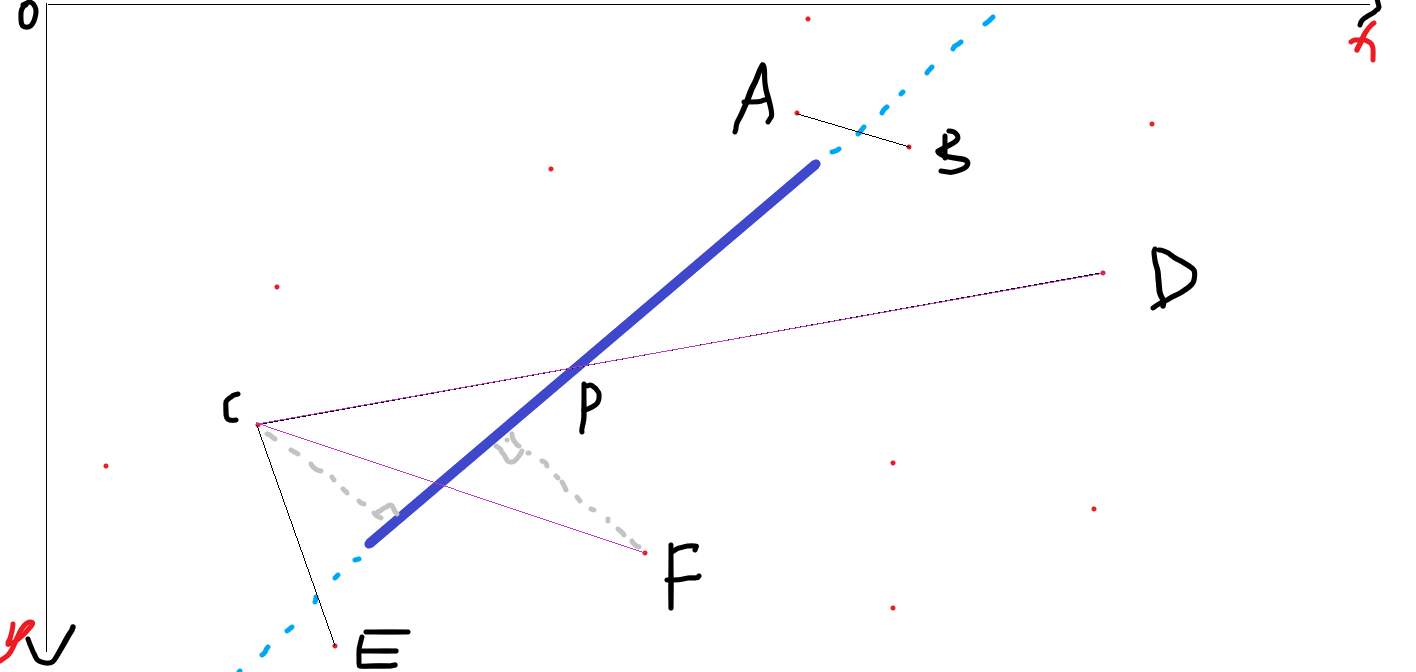
Say I got a bunch of points(red points) and a blue line segment, i want to find a line(2 points) which is intersect with the blue line segment and the sum of two end points' perpendicular distance to the blue line segment is the shortest distance .

P in this picture above is CD and the blue line segment intersect point.

I only know that they should be on the blue line's different side (left/right or above/below).

But there are still serveral variants can make this go south.Like AB and CE in this picture.

Edit : At first i thought i only need to make sure both of two end points' projection point lies on the blue line segment.But if I do so,there might be not so many good points for this case.I might just throw the only solution away.

Edit2 : The background is about image processing.Find 2 reliable points (say line M) near given line segment say L,if they intersect with each other then in another image they still does.It's about find line L's candidates in another image.

Edit3 : Some python codes,but it's just my first thought.

It's not finished so it's not tested yet.

class Point:
    def __init__(self):
        self.point = (0, 0)
        self.dist = float(Inf)

    def update(self, point, dist):
        self.point = point
        self.dist = dist


    for l0 in lines0:
        # contains shortest perpendicular distance point on each side
        temp = [Point(), Point()]
        for p0 in points0:
            x1, y1, x2, y2 = l[0]
            # define given line L
            line = lsrl.Line(lsrl.Point(x1, y1),
                             lsrl.Point(x2, y2))

            # define point from points
            point = lsrl.Point(p0[0], p0[1])

            # perpendicular distance
            dist = lsrl.distToLine(line, point)

            # which side on return 0,1,2
            side = lsrl.determineSide(line, point)
            # lies on the given line
            if side == 2:
                pass
            if dist < temp[side].dist:
                # meet a better point then update
                temp[side].update(p0, dist)

CodePudding user response：

Sketch of algorithm:

1. Calculate all perp. distances including orientation (left or right of dividing line L).
2. Devide points in two lists (left or right).
3. Sort both lists by perp. distance.
4. Now build pairs from both lists, sorted by minimal sum of perp. distance.
5. Choose the first (smallest sum) pair with a connecting line that intersects L as result.