Binary Asymmetric Matrix of Size 100 with Numpy-CodePudding

please take it easy, I'm new to Python and new to this site. I'm trying to create a random, 100 by 100 binary matrix using numpy. It's supposed to represent a co-citation network, so cycles aren't allowed (basically the matrix has to be asymmetrical across the diagonal, at least for nonzero values.

import numpy as np
n=100
array = np.random.randint(0,2,size=(n,n))

for i,j in range (0,n):
        if A[i][j] == 1:
                A[j,i] == 0


print(array)

CodePudding user response：

A directed graph whose adjacency matrix is asymmetrical in the sense you described will not be in general acyclic. It will not have cycles of length 2, but it can have longer cycles e.g. 1 -> 2 -> 3 -> 1.

Any directed acyclic graph can be represented by a lower triangular adjacency matrix by rearranging its nodes in an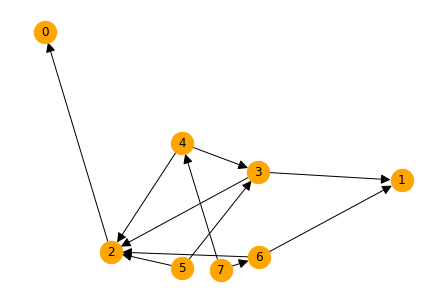

If you want to obtain an adjacency matrix which represents a directed acyclic graph but it is not in the lower triangular form, you can reorder the nodes in some random order. This amounts to selecting a random permutation of node indices and conjugating the above adjacency matrix by the resulting permutation matrix:

#a random permutation of nodes
p = rng.permutation(range(N)) 
#the permutation matrix
P = np.zeros((N, N), dtype=int)
P[np.r_[:N], p] = 1
#conjugate the adjacency matrix A by P
new_A = P@[email protected]
print(new_A)

This gives:

[[0 0 1 0 0 0 0 1]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 1 0 1 0]
 [0 0 0 0 1 0 1 0]
 [0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0]
 [0 1 0 0 1 0 0 0]
 [0 1 0 0 1 0 0 0]]

CodePudding user response：

thanks for the response, I think the cycle longer cycles will work, for example if A cites B and B cites C, then A can cite C, then A can cite C as long as they are not both citing each other. The biggest problem was that obviously you can't have instances where the citations don't follow chronological order.