Problem with plotting multiple functions with a for loop in matplotlib-CodePudding

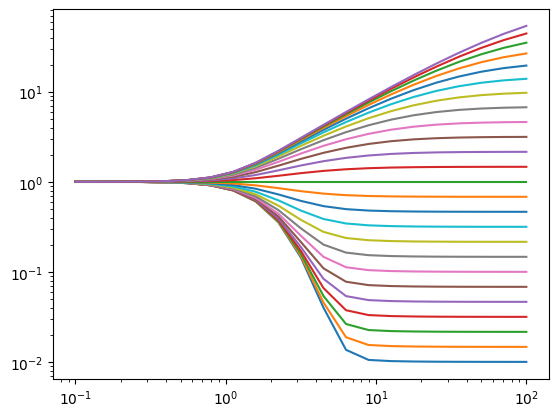
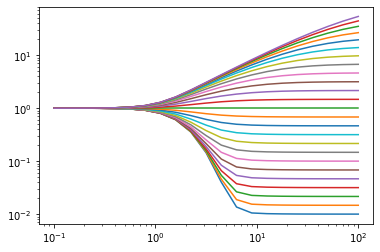
I am using a for loop to plot a curve for each parameter-value (k) - this works just fine for all the negative k-values, but when the loop reaches the k values = 0 or greater, the lambdify function seems to collapse and I get an error stating the dimensions of x and y are not equal.

This is my code:

import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

eta = np.logspace(-1,2,21) #defines eta values, 21 decades from 0.1 to 100
relrho = np.logspace(-2,2,25) #defines values of rho2/rho1, 25 values from 0.01 to 100
k = (relrho-1)/(relrho 1) #defines the reflection coefficient

#parameter of type curve is k
#rhoa/rho1 is the y-axis
#eta is the x-axis

#R is assigned as the ratio of rho_a to rho_1
#x is assigned to eta
#y is assigned to k

x = sym.symbols('x', real = True)
y = sym.symbols('y')

for y in k: #for-loop assumes k value before while-loop is run, then plots the curve, then new k value is assumed
    n=1; R=1;
    while n<=500:
        Rnew = 2*x**3*y**n/(((2*n)**2 x**2)**(3/2))
        R = R   Rnew
        n = n   1
    R = sym.lambdify(x,R)
    plt.loglog(eta, R(eta))
plt.show()

What is going wrong? I am completely at a dead end right now... clueless...

If I plot the curves individually I can plot them for any k-value just fine, but in the loop it collapses after 12 iterations.

runfile('C:/Users/aslak/OneDrive/Desktop/Typecurves.py', wdir='C:/Users/aslak/OneDrive/Desktop')
Traceback (most recent call last):

  File "C:\Users\aslak\OneDrive\Desktop\Typecurves.py", line 44, in <module>
    plt.loglog(eta, R(eta))

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\pyplot.py", line 2750, in loglog
    return gca().loglog(*args, **kwargs)

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_axes.py", line 1868, in loglog
    return self.plot(

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_axes.py", line 1743, in plot
    lines = [*self._get_lines(*args, data=data, **kwargs)]

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 273, in __call__
    yield from self._plot_args(this, kwargs)

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 399, in _plot_args
    raise ValueError(f"x and y must have same first dimension, but "

ValueError: x and y must have same first dimension, but have shapes (21,) and (1,)


runfile('C:/Users/aslak/OneDrive/Desktop/Typecurves.py', wdir='C:/Users/aslak/OneDrive/Desktop')
Traceback (most recent call last):

  File "C:\Users\aslak\OneDrive\Desktop\Typecurves.py", line 34, in <module>
    plt.loglog(eta, R(eta))

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\pyplot.py", line 2750, in loglog
    return gca().loglog(*args, **kwargs)

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_axes.py", line 1868, in loglog
    return self.plot(

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_axes.py", line 1743, in plot
    lines = [*self._get_lines(*args, data=data, **kwargs)]

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 273, in __call__
    yield from self._plot_args(this, kwargs)

  File "C:\Users\aslak\anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 399, in _plot_args
    raise ValueError(f"x and y must have same first dimension, but "

ValueError: x and y must have same first dimension, but have shapes (21,) and (1,)

CodePudding user response：

The problem is that when y=0, then 2*x**3*y**n/(((2*n)**2 x**2)**(3/2)) will be 0, hence R will be zero. When you lambdify it and pass in a numpy array, it will return the scalar value 0. We need to take into account this fact. Note that in the following code block I also optimize for speed: only one symbolic addition will be executed for every iteration of the for loop.

import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

eta = np.logspace(-1,2,21) #defines eta values, 21 decades from 0.1 to 100
relrho = np.logspace(-2,2,25) #defines values of rho2/rho1, 25 values from 0.01 to 100
k = (relrho-1)/(relrho 1) #defines the reflection coefficient

#parameter of type curve is k
#rhoa/rho1 is the y-axis
#eta is the x-axis

#R is assigned as the ratio of rho_a to rho_1
#x is assigned to eta
#y is assigned to k

x = sym.symbols('x', real = True)
y = sym.symbols('y')

for y in k: #for-loop assumes k value before while-loop is run, then plots the curve, then new k value is assumed
    print("y", y)
    n=1; R=1;
    addends = []
    while n<=500:
        addends.append(2*x**3*y**n/(((2*n)**2 x**2)**(3/2)))
        n = n   1
    R = Add(R, *addends)
    R = sym.lambdify(x,R)
    R_val = R(eta)
    if not hasattr(R_val, "__iter__"):
        R_val = R_val * np.ones_like(eta)
    plt.loglog(eta, R_val)
plt.show()

CodePudding user response：

Davide_sd pointed out why the code fails, but in this case it is faster to avoid sympy altogether:

import numpy as np
import matplotlib.pyplot as plt

eta = np.logspace(-1, 2, 21)
relrho = np.logspace(-2, 2, 25)
k = ((relrho - 1) / (relrho   1))
n = np.r_[1:501]

y = k[None, :, None]
x = eta[:, None, None]
R = (2 * x**3 * y**n / (((2 * n)**2   x**2)**(3 / 2))).sum(axis=2)   1
plt.loglog(eta, R)
plt.show()