Print all the subarrays with unique K different elements-CodePudding

I came across 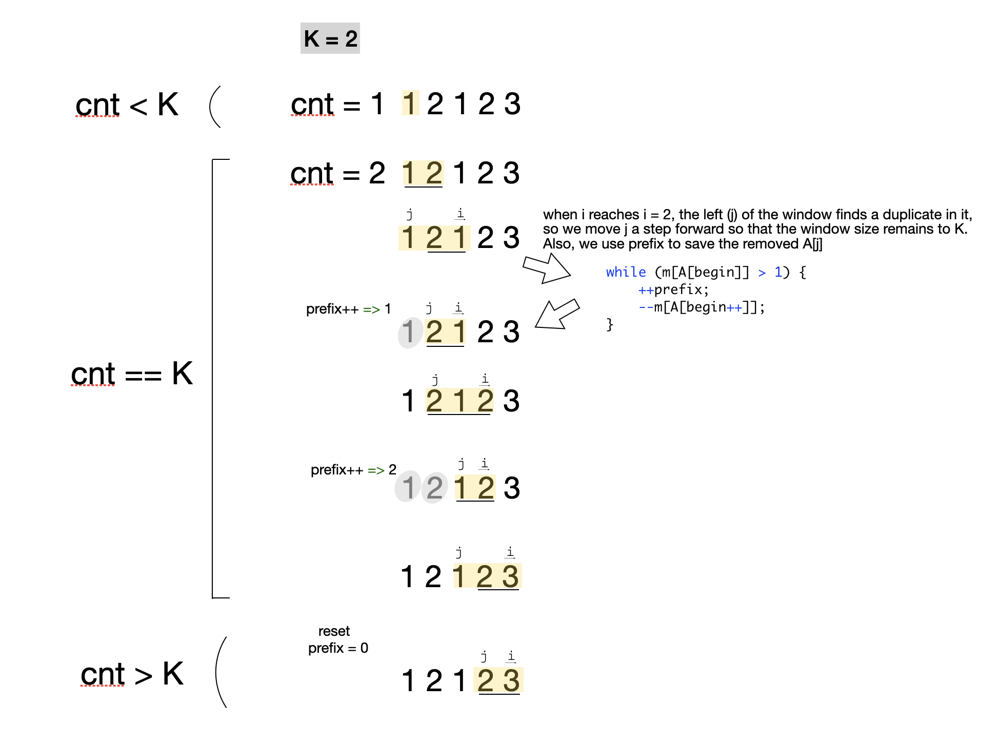As shown in the picture above it get the sub-array with elements

[1, 2]
[1, 2, 1]
[2, 1]
[2, 1, 2]
[1, 2]
[2, 3]

However I fail to understand how to get the subarray with the elements {1, 2, 1, 2}

As, the subarrays formed with exactly two elements are:-

[1, 2]
[1, 2, 1]
[2, 1]
[2, 1, 2]
[1, 2]
[2, 3]
[1, 2, 1, 2]

this is my solution

import java.util.*;

public class Main {
    public static void main(String[] args) {
        int[] A = {1, 2, 1, 2, 3};
        int K = 2;

        HashMap<Integer, Integer> map = new HashMap<>();
        ArrayList<Integer> list = new ArrayList<>();

        
        for(int i = 0;i<A.length; i  ){
            map.put(A[i], map.getOrDefault(A[i], 0)   1);
            list.add(A[i]);

            if(map.size() == K) System.out.println(list);

            while(map.get(list.get(0)) > 1 || map.size() > K){
                map.put(list.get(0), map.get(list.get(0)) - 1);
                if (map.get(list.get(0)) == 0) map.remove(list.get(0));
                
                list.remove(0);
              
                if(map.size() == K) System.out.println(list);
            }
        }
    }
}

which gives the output

[1, 2]
[1, 2, 1]
[2, 1]
[2, 1, 2]
[1, 2]
[2, 3]

But I am failing to understand how to include {1, 2, 1, 2} with this method. Where am I going wrong !

CodePudding user response：

The first thing that I'm noticing is that both of the questions you've referenced are about finding the count of the subarrays with K unique elements, not printing them as you're trying to do here. It's a difference that can affect the way the code is read and understood, and worth pointing out :)

As to how [1, 2, 1, 2] could be included in the result, I reviewed the GeeksForGeeks link that you included. The main point from it that I picked up and that seems to be missing from your code is the idea of the prefix.

As seen in the image you posted above, the main logic of the algorithm keeps track of the sliding window. Since the algorithm is looking for subarrays with no more than K elements, it limits the size of the sliding window to K at the end of each iteration of the loop. Due to this, there needs to be a way to keep track of the case where elements are duplicated - otherwise, the algorithm wouldn't count subarrays with more than K total elements, but duplicates of the K unique elements.

This is where the prefix comes in. As you can see in the picture you posted above, the algorithm includes checking the contents of the sliding window every time it increases to a size greater than K.

If the window has more than K elements because it contains duplicate elements, then the first element is separated as a "prefix" (or added to it if one already exists). This keeps the size of the window limited to K, while also tracking that the prefix is still a valid part of the sub-array. The size of this prefix is then tracked as the window continues to slide. For each new valid subarray that the algorithm finds, it increases the total count of valid subarrays by 1 (for the new K-lengthed subarray) plus the length of the prefix. This is because each subarray that can be constructed from the prefix, when combined with the current sliding window, is still a subarray of K unique elements. This is how [1, 2, 1, 2] is counted in the algorithm - when i = 5, the "sliding window" is [1, 2] (the second occurrence of each number in the input list), and the prefix size is 2 - representing the list of [1, 2] (the first occurrence of each number in the input list). So, the total number of valid subarrays at this point in the algorithm is 3 - [1, 2] (the sliding window), [2, 1, 2] (the sliding window prepended with the last element of the prefix), and [1, 2, 1, 2] (the sliding window prepended with the entirety of the prefix).

If the window has more than K elements simply because each element is unique, then the algorithm knows that it's hit the end of a valid subarray - both the current window and any of the subarrays that prepend part of the prefix to it will always have more than K unique elements. At that point, the algorithm resets the prefix, shrinks the window to K elements, and continues processing.

CodePudding user response：

Here's a linear approach.

Use two indices, a counter for the number of distinct elements between your indices, and a counting map (from element to count between indices).

When the number of distinct elements is <= your target:
1) print if you have equality
2) increment the right index
3) update the counting map
4) increment the number of distinct elements if step 3 took something from zero or uninitialized to 1.

When the number of distinct elements is > your target:
1) increment the left index
2) update the counting map
3) decrement the number of distinct elements of step 2 to something from 1 to zero.