find unique neighbour pairs between two point clouds in R-CodePudding

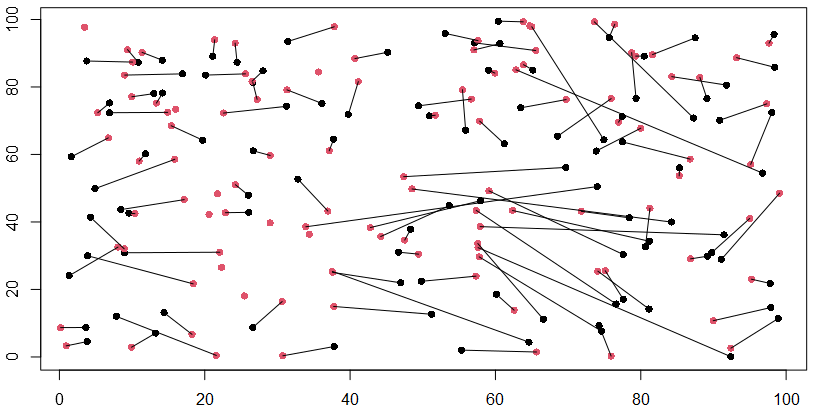
Given two point clouds I want to find for each point from the first point cloud the nearest neighbour from the second point cloud. Also, each pair of neighbours should be unique. The solution was already given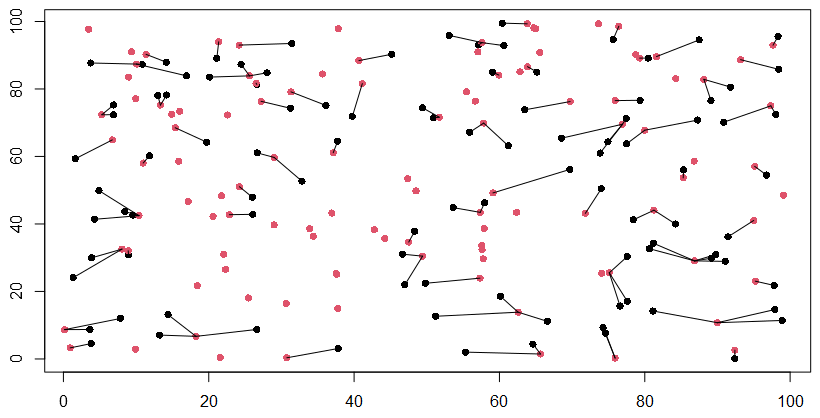

As shown in the image above, I'm capable of finding the nearest neighbour for each point from Point Cloud 1 (black) to Point Cloud 2 (red). Yet, multiple points from Point Cloud 2 are assigned to the same point from Point Cloud 1. Any idea how to find unique pairs with minimal overall distances instead?

Edit:

I tried another approach by finding the closest pair iteratively and removing that pair from the following queries:

# Approach 2:

pairs = matrix(NA, ncol = 4, nrow = nrow(pc1)) #storage for pairs
colnames(pairs) = c("x(pc1)", "y(pc1)", "x(pc2)", "y(pc2)")

pc2_copy = pc2 # copy of Point Cloud 2 which will shrink each iteration

for(i in 1:nrow(pc1)){
  nn = get.knnx(pc2_copy, pc1[i,,drop = FALSE], k = 1)
  pairs[i,1:2] = pc1[i,1:2,drop = FALSE]
  pairs[i,3:4] = pc2_copy[nn$nn.index[1,1],1:2,drop = FALSE]
  pc2_copy = pc2_copy[-c(nn$nn.index[1,1]),] #remove the corresponding point from the matrix
}

plot(pc1, pch = 16, col = 1)
points(pc2, pch = 16, col = 2)

for(i in 1:nrow(pairs)) lines(x = pairs[i,c(1,3)], y = pairs[i, c(2,4)])

While this gives me unique pairs, I don't believe this is anywhere near an ideal solution (in my real data example some distances are very little while others are immense with an obviously much better solution by eye).

CodePudding user response：

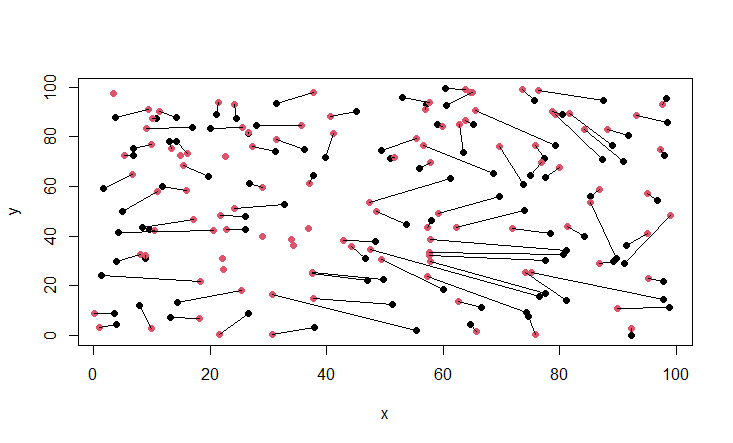
The package RcppHungarian will solve this type of assignment problem using the Hungarian algorithm:

set.seed(666)

# Example data
px = runif(210, min = 0, max = 100)
py = runif(210, min = 0, max = 100)

pc1 = cbind(x = px[1:100], y = py[1:100])
pc2 = cbind(x = px[101:210], y = py[101:210])
nn <- RcppHungarian::HungarianSolver(
  proxy::dist( # distance matrix
    pc1, pc2, method = "euclidean"
  )
)$pairs
any(duplicated(nn[,2]))
#> [1] FALSE
plot(pc1, pch = 16, col = 1)
points(pc2, pch = 16, col = 2)
for(i in 1:nrow(pc1)) lines(x = c(pc1[i,1], pc2[nn[i,2],1]),
                            y = c(pc1[i,2], pc2[nn[i,2],2]))