I'm working on a piece of legacy software, which has code that takes a mesh/3d point/radius/direction, and computes a list of vertices that are selected.

public static List<int> GetSelectedVertices(PointCloud model, Vec3 markPoint, Vec3 direction, float selectionRadius)
 {
     List<int> outputVertices = new List<int>();
     Vec3 normal = GetNormal(direction);
     foreach(int vertexId in model.VertexIds)
     {
         Vec3 facetPosition = model.GetFacetPosition(vertexId);
         Vec3 vec3d = facetPosition - markPoint;
         
         var computation = vec3d.X * vector3.X   vec3d.Y * vec3d.Y   vec3d.Z * vec3d.Z - 
            FloatSquare(vec3d.X * normal.X   vec3d.Y * normal.Y   vec3d.Z * normal.Z)
            
        if(computation < selectionRadius)
        {
            outputVertices.Add(vertexId);
        }
     }
     
     return outputVertices;
 }
 
 public static float FloatSquare(float input)
 {
     return input * input;
 }
 
 public static Vec3 GetNormal(Vec3 input)
 {
     double num = 1.0 / Math.Sqrt(input.X * input.X   input.Y * input.Y   input.Z * input.Z);
     return new Vec3(num * input.X, num * input.Y, num * input.Z);
 }

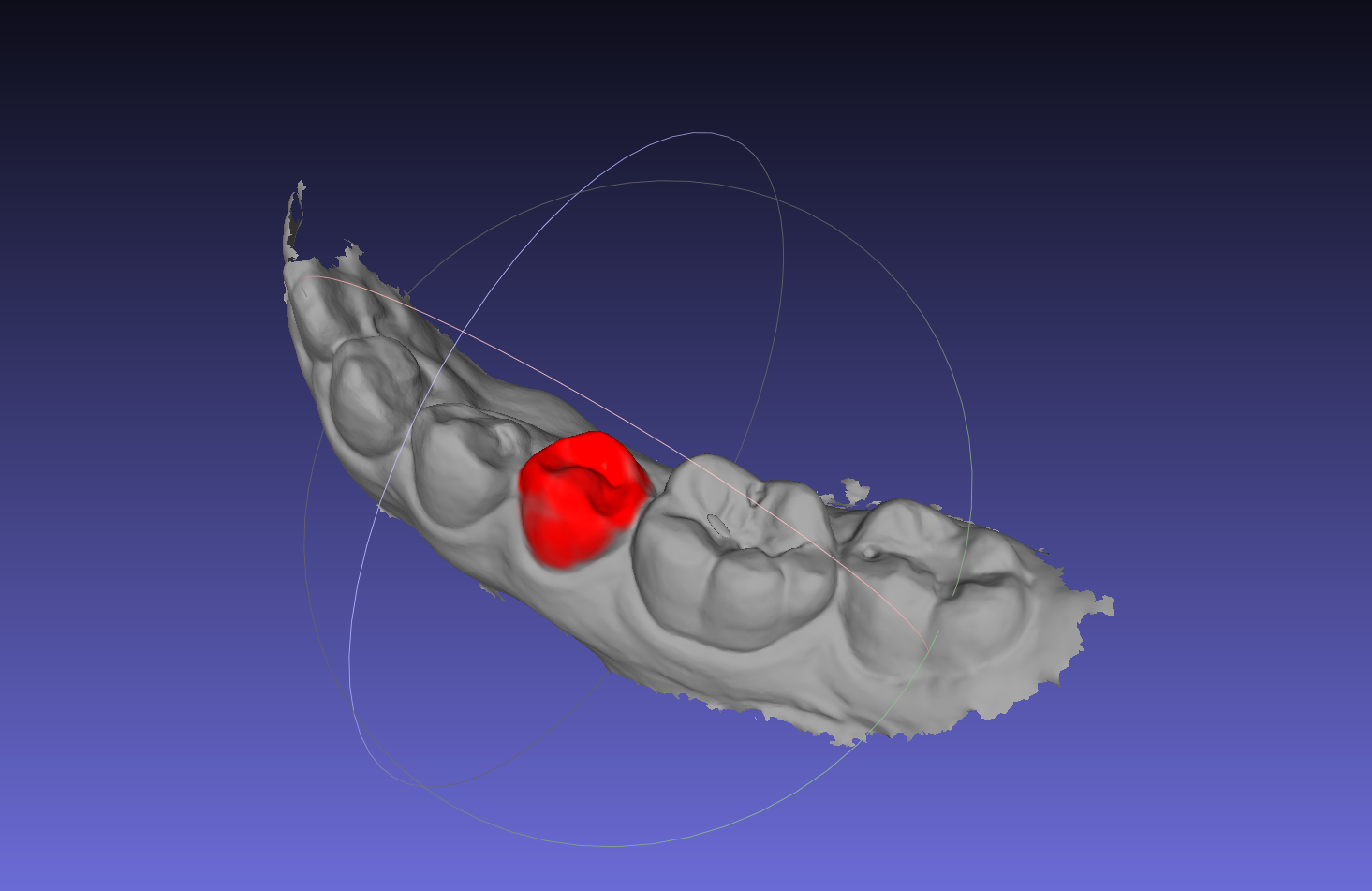
Given a list of vertices and their positions(highlighted in red in the image below, I want to compute a 3D point & radius that would allow GetSelectedVertices to encompass as many of the input vertices as possible, while minimizing inclusion of unnecessary vertices(i.e. any vertices that are not highlighted in red). Also, the ability to define a maximum radius would be extremely helpful.

Unfortunately I'm not allowed to change the GetSelectedVertices implementation, and minimizing the selection of unnecessary vertices is highly important.

I've currently tried two approaches, with lackluster results:

1. Divide and conquer approach, where I split a bounding box into tiny segments and try each one(too slow, and suboptimal)
2. Selecting the highest vertex, or the vertex closest to the bounding box center(too inaccurate)

Are there any well-known solutions to similar problems, or other approaches I could take?

Edits:

1. Encompassing some unselected vertices is perfectly ok, but there is a cost to them. As a heuristic, something like 20% growth is acceptable. I.e. If you were to grow my selection by 20%, any newly selected facets are perfectly fine to encompass.

CodePudding user response：

I would ignore mesh data and use just PCL (points)... first I would start with:

1. set center to avg point of selected points
2. set radius that is minimal and encloses all selected points

Now you can exploit tooth geometry if you know the orientation of tooth main axis then the center of bounding sphere will lie on it (tooth central axis) so you just fit the center position along this axis in direction from avg point upwards for lower teeth and downwards fro upper teeth. So you end up with just 2 nested fits.

For that you can use search like this:

• approximation search

and use number of unselected points inside bounding sphere as error function for the fit of center and radius size for the radius fit.

The max values for the search can be obtained from BBOX size (some safe multiple of it)

btw I already dealt with similar problem (also for teeth scan like this) however it was in chat only see:

• my old chat about teeth segmentation

If you go through the whole stuff there are ideas and IIRC also code for obtaining the tooth axis (have also found my original project for it)

CodePudding user response：

Use logistic regression. If O = (Ox, Oy, Oz) is the unknown center of the sphere and R is the unknown radius, then define the quadratic function

S(x, y, z, Ox, Oy, Oz, R) = (x - Ox)^2 (y - Oy)^2 (z - Oz)^2 - R^2

To abbreviate the notations, let P = (x, y, z) and O = (Ox, Oy, Oz) so the function S can be denoted as

S(x, y, z, Ox, Oy, Oz, R) = S(P, O, R) = ||P - O||^2 - R^2

Let the 3D data points be P[1], P[2], ..., P[i], ..., P[n] labeled y[1], y[2], ..., y[i], ..., y[n] where y[i] = 1 if the point P[i] is red point, i.e. a point that should be inside the sphere, while y[i] = 0 if the point P[i] is not red, i.e. it should be grey and should be outside the sphere.

Form the logistic regression function

f(P, O, R) = 1 / (1 exp( S(P, O, R) )) = 1 / (1 exp( ||P - O||^2 - R^2 ))

With its help, form the maximum likelihood function

L(O, R) = sum{i=0 to n} y[i] * ln( f(P[i], O, R) ) (1 - y[i]) * ln( 1 - f(P[i], O, R) )

Find (O, R) that maximize the function L(O, R), i.e. solve

(Ox, Oy, Oz, R) = argmax L(Ox, Oy, Oz, R)

This is frequently done by gradient descent method, i.e. you want to solve the system of equations

grad L(O, R) = 0

or component-wise:

d/dOx( L(Ox, Oy, Oz, R)  )  = 0
d/dOy( L(Ox, Oy, Oz, R)  )  = 0
d/dOz( L(Ox, Oy, Oz, R)  )  = 0
d/dR ( L(Ox, Oy, Oz, R)  )  = 0

and therefore you iterate

h = small step
while ||grad L(O, R)||^2 > very small number:
   (O, R)  =  (O, R)  - h * grad L(O, R)

For more details on logistic regression and some more formulas, see the logistic regression Wikipage.